Sun Angle and Beam Concentration
If every beam of sunlight reaching Earth has the same amount of energy, why do some areas warm up more than others? To answer this thoroughly, we need to analyze an area’s energy budget: CRACL (Conduction, Radiation, Advection, Convection, and Latent Heat). But since it all starts with the Sun’s radiation reaching Earth, let’s focus on the concentration of sunlight reaching the ground, which depends on the angle of the sun above the horizon, or sun angle, regardless of one’s latitude, day of the year, and time of the day.
Click the button to run the web app for desktops, laptops, tablets, and smartphones.
There is supporting information for the app below and a second button to run the app.
The Sun emits near-constant electromagnetic energy (radiation), and how it intersects with the Earth’s surface determines how it heats. The warmed surface, in turn, warms the air. Imagine a beam of sunlight that has a circular cross-section shining perpendicularly onto the ground. The area of the illuminated ground is the same as the area of the sunbeam. If this same beam hits the ground at a 30° angle, the circular beam of light illuminates an elliptical patch of ground. The ellipse has a major axis twice as large as the sunbeam’s diameter, yet the minor axis remains the same as the sunbeam’s diameter. The ellipse’s area is twice as large as the sunbeam, so the beam’s energy is spread out over twice as large an area, or the beam concentration is 0.5 (Figure 1). We will call the ratio of the sunbeam’s cross-sectional area to the area of the illuminated ground area beam concentration (Table 1).
If the Sun is on the horizon, the rays don’t hit the ground (they are parallel to it), so the beam is spread out over an infinite piece of real estate, and the beam concentration equals 0%. When the Sun is directly overhead or at the zenith, the beam’s size is the same size illuminating the ground, so the beam concentration is 100%.
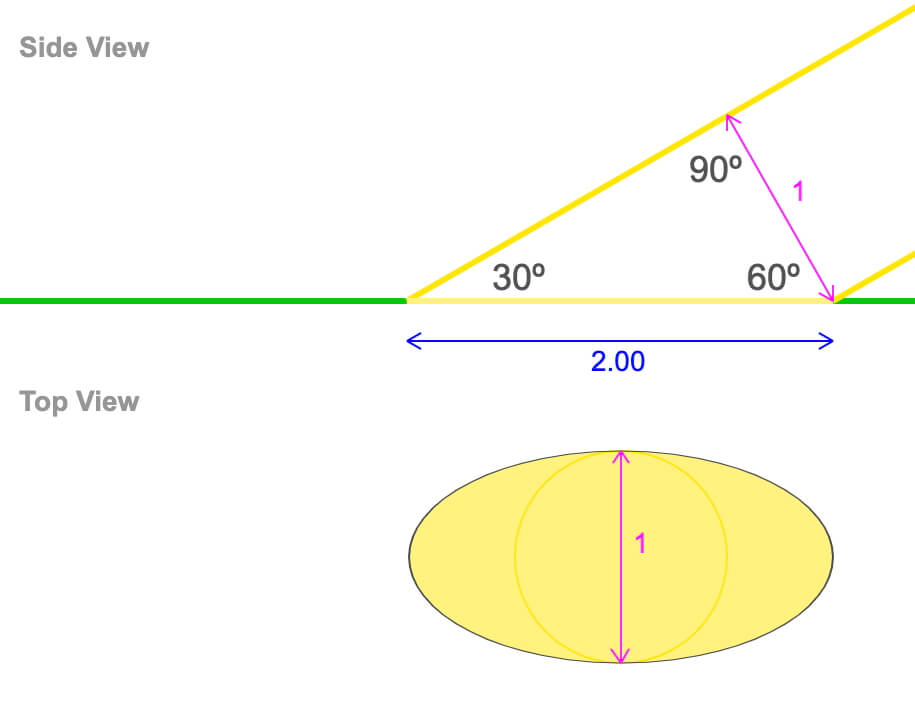
Figure 1. A circular sunbeam with a cross-sectional diameter of 1 unit hits the ground at 30°. The illuminated ellipse on the ground has a major axis twice as large as the beam’s diameter, but its minor axis is the same as the sunbeam’s diameter.
Hands-On Activities
Shine a flashlight onto a horizontal piece of paper or book. Slowly tilt the book but keep the axis of rotation the same distance from the flashlight. The beam of light elongates but doesn’t widen. An experiment with more accessible technologies uses three pencils to measure a beam of sunlight’s elongation as the sun angle changes. Be creative with the pencils to show that the illuminated surface’s width remains constant as the sun angle changes.
Calculating Beam Concentration
We will use the ellipse created when a circular beam of sunlight intersects the flat, level ground at 30º above the horizon (as shown in the following illustration).
Beam Concentration = Cross-Sectional Area of Sunbeam / Area of Illuminated Ground
where the
Area of Sunbeam = Area of a Circle
= π (Diameter/2)²
Area of the Illuminated Ground = Area of Ellipse
= π (Major Axis/2) (Minor Axis/2)
Since the beam of sunlight has a diameter of 1 unit and its angle to the ground is 30º, then the axes of the illuminated ellipse are:
Minor Axis = Circle Diameter = 1 and
Major Axis = Circle Diameter / sin(30º) = 1 / (1/2) = 2
Then,
Beam Concentration = π (1/2)² / (π (2/2) (1/2)) = 2
We can write a general equation for beam concentration:
Beam Concentration = π (Radius)² / (π (Radius / sin(Sun Angle)) (Radius)) or
Beam Concentration = sin(Sun Angle)
This implies that the sunbeam’s cross-sectional shape is unimportant; all we need to know is the Sun’s angle above the horizon! What happens if you use a square beam of sunlight? Test the conclusion that the sunbeam’s shape does not affect the beam concentration (view this scenario using the Beam Concentration web app available below).
If you are unfamiliar with the sine function, see Right Triangles and Vectors.
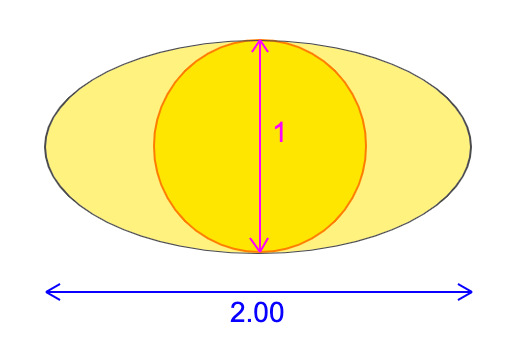
Above is an illustration of how a beam of sunlight (dark yellow) spreads out over the illuminated ground (light yellow) when it shines at an angle of 30º to the surface. Notice that the circular sunbeam creates an ellipse of illuminated ground where the minor axis (the shortest axis that is perpendicular to the elongation) remains the diameter of the sunbeam.
| Sun Angle above Horizon | Concentration of Sunlight Illuminating the Ground |
| 90º | 100% |
| 80º | 98.48% |
| 70º | 93.97% |
| 60º | 86.60% |
| 50º | 76.60% |
| 40º | 64.28% |
| 30º | 50.00% |
| 20º | 34.20% |
| 10º | 17.36% |
| 0º | 0% |
Table 1. When the Sun is higher in the sky, a beam of sunlight illuminates a smaller area of ground, so the intensity of sunlight within the smaller area is more concentrated than when the Sun is lower in the sky.
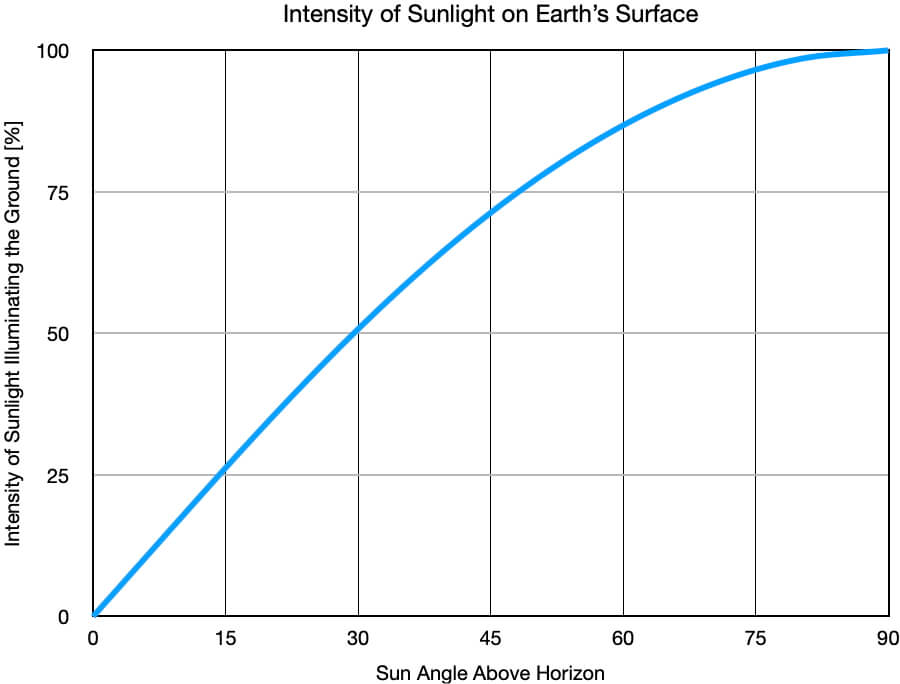
Figure 2. The intensity of sunlight illuminating horizontal ground depends on how high the Sun is in the sky (sun angle).
When the Sun is high in the sky, the energy of a beam of sunlight is more concentrated on level ground. More energy reaches a unit area of land compared to when the Sun is lower in the sky. As we saw with the black fabric experiment and the diurnal heating patterns, the more radiation absorbed by a surface, the greater the temperature change. Beam concentration is an important variable that determines a location’s daily and seasonal temperature patterns.
Use the Web App to Explore Beam Concentration
If you would like to explore the relationship of beam concentration and the Sun’s angle above the horizon in more detail, run the web app, Beam Concentration, below.
Click the button to run the web app for desktops, laptops, tablets, and smartphones.
Acknowledgments
Thanks to Matti Horne for her suggestions during beta testing and for designing our new certificate of completion. Alan Gould’s insightful suggestions led to a revision of the webpage and several changes in the web app after its initial release, including adding a square beam of sunlight.
The Shape of Sunbeams
Why are two shapes of sunbeams used in the web app? If you’ve played with a flashlight or a laser, the shape of the beam of light is almost always circular, so conceptually, this may be easier to consider first. However, if you want to calculate the total amount of the Sun’s energy reaching Earth’s surface, you need to use square sunbeams since there won’t be any gaps between adjacent sunbeams reaching the ground.
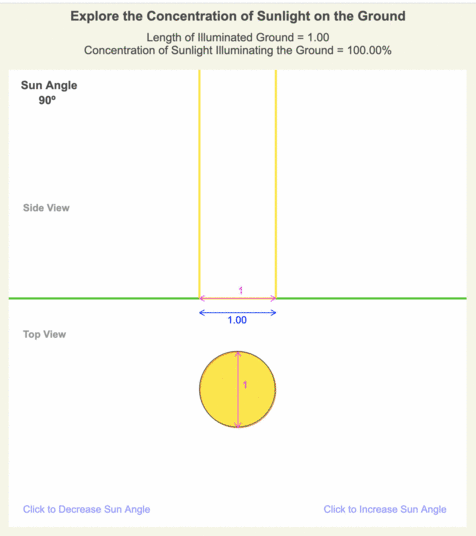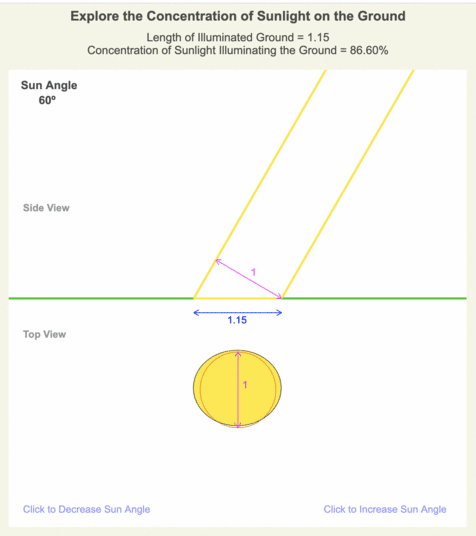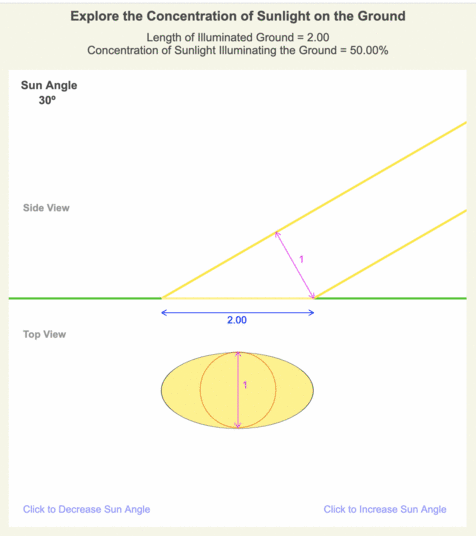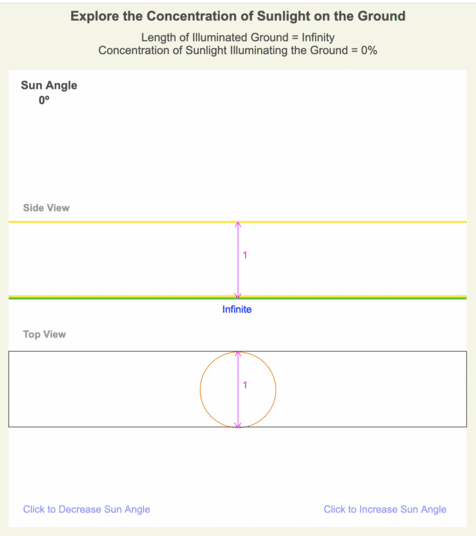
An animation of screenshots from the Beam Concentration web app is shown. The app allows you to change the viewing perspective and to turn data on and off. The ellipse’s shade of yellow indicates the intensity of the sunlight illuminating the ground, and the length of the ellipse’s major axis determines the beam concentration. For scale in the top view, the sunbeam’s size at a 90º sun angle is drawn in orange.
Calculate the Times and Hours the Sun is Above Selected Angle
Combine the beam concentration with sun angle with the following app that calculates the number of hours the sun is above a selected angle for each day of the year for a selected latitude. Use this Google Sheets document: Times and Durations when Above Sun Angle. Below are examples of data and graphs you may create using the app.
The file will open in Google Sheets, then use the “Make a Copy” in the File Menu so you may change the latitude and sun angle to calculate and graph a year of times and durations the sun will be above the angle. Tip: the name of your file should include what experiment(s) you are trying.
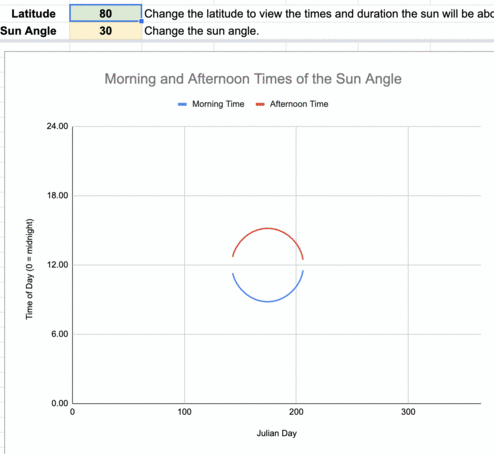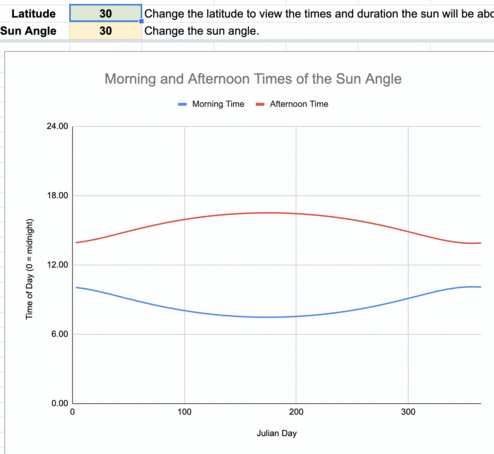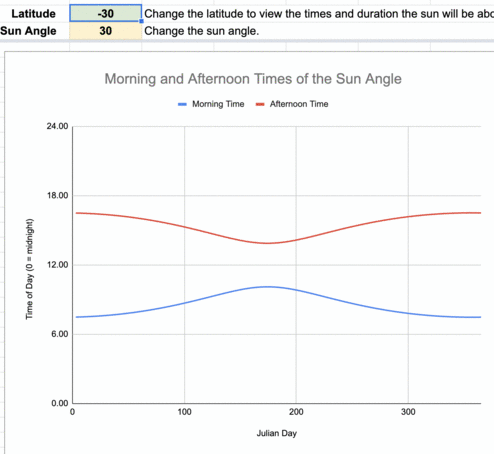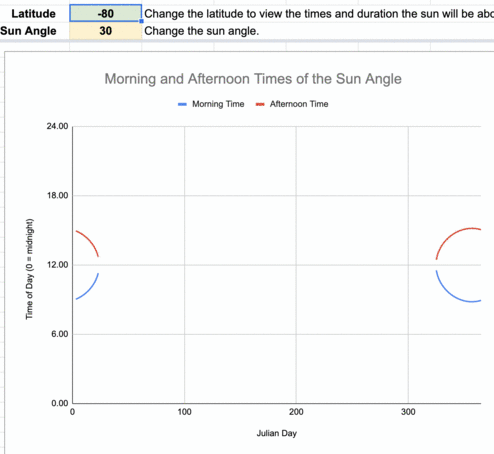
Animation of the times of the day when the sun reaches 30º in the sky for every 10º of latitude. The blue line represents the times this occurs before noon, and the red line shows the times after local noon.
At 30º sun angle, the beam concentration is 50%.
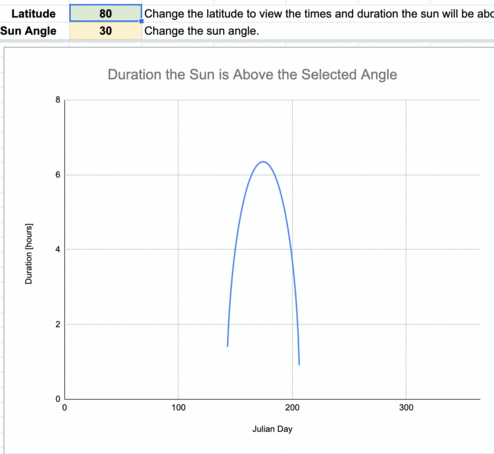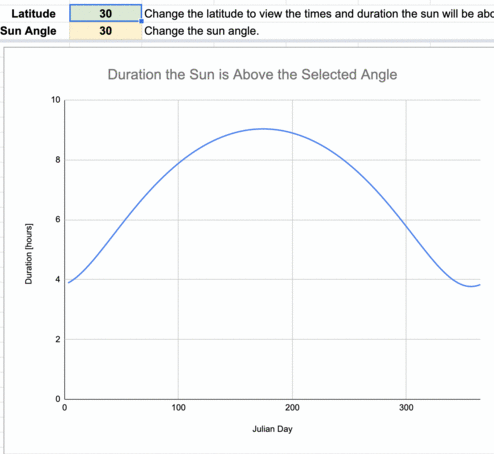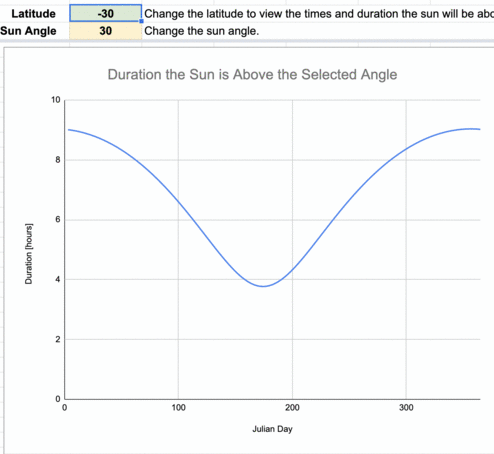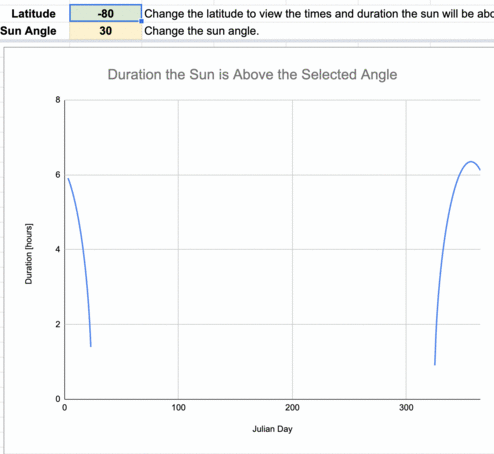
Animation of the daily number of hours the sun is at least 30º above the horizon for every 10º of latitude.
The lower latitudes (those near the equator) have more consistent daily durations when the sun is at least 30º above the horizon throughout the year compared to higher latitudes. There are an increasing number of days when the sun is never greater than 30º above the horizon the farther you are from the equator. Poleward of 83.5ºN/S, the sun is never above 30º above the horizon during the year.
Use the spreadsheet to continue exploring the distribution of sunlight concentration throughout the year around our planet.
There are two sheets to the document:
-
- Input and Output: Change the latitude (light green box) and sun angle (light yellow box) on this sheet and automatically see the graphs update.
- Calculations: See the daily data in table form on this sheet, plus explore the formulas used to calculate the times and durations the sun is at and above the selected angle.
Big Ideas
- The Sun emits near-constant electromagnetic energy (radiation), and how it intersects with the Earth’s surface determines how the ground/water heats, and the warmed surface, in turn, warms the air.
- As the sun gets closer to the horizon, the beam of sunlight illuminates a longer stretch of terrain, yet the width remains the same.
- The sun angle above the horizon determines the concentration of the Sun’s radiation on the Earth’s surface, which is an important variable that determines a location’s daily and seasonal temperature patterns.
Click on the following toggles to view descriptions and links of the web pages on each topic of the Sun-Earth Connection.
Sun-Earth Connection overview
An overview of how the Sun’s energy is generated and how its thermal radiation illuminates and heats Earth.
Earth Illumination Patterns
- Overview: The Sun illuminates the spherical, rotating planets orbiting it.
- Obliquity and Earth’s Illumination: Obliquity is the angle between the planes of the Earth’s equator and its orbit around the Sun.
- Declination, Latitude, & Earth Illumination: Solar declination is the angle between the Sun’s rays and the plane of the Earth’s Equator. Its value depends on where Earth is in its orbit around the Sun.
- Astronomical Seasons & Illumination: Astronomical seasons are based on the orientation of Earth’s axis of rotation to the Sun, which determines the amount of illumination between the Northern and Southern Hemispheres.
Distribution of the Sun's Energy on Earth
- Overview: Even though an area is illuminated by sunlight, there can be quite a range of energy interacting with the surface.
- Sun Angle and Beam Concentration: If every beam of sunlight reaching Earth has the same amount of energy, why do some areas warm up more than others?
- Diurnal Heating: Diurnal heating is the temperature change over 24 hours. When sunlight shines on the ground, it warms. Two critical factors that determine the amount of heating deal with the Sun’s illumination.
- Seasons: Earth experiences astronomical seasons due to its obliquity.
- Climate Regimes: Climate regimes are an extension of diurnal heating and seasons, but the time frame is now years.
Declination Circles: A tool to analyze the Sun's position in the sky.
- Overview: Drawings of declination circles contain the visual and numerical information to understand and predict the Sun’s motion across the sky.
- Declination Circles 101: Draw a declination circle with just a ruler and protractor/compass to quickly and accurately know the Sun’s position in the sky at any day and time of the year for any location on Earth.
- Drawing Declination Circles: Declination circles are quite easy to draw by hand.
- Interpreting Time on Declination Circles: Accurately estimate the time of day using the Sun’s location in the sky.
- Sunrise, Sunset, & Twilight: Calculate the timing and duration when the Sun is at or near the horizon.
- Solar Time, Angle, & Position: The sun’s angle and direction to the local horizon define the Sun’s position in the local sky. Explore how to use declination circles to calculate the Sun’s position at any solar time anywhere in the world on any day of the year.
- Changing Views of Declination Circles: Use the web app View Declination Circles to explore three common views of declination circles to identify their strengths, limitations, and applications. Then learn how to go from one view to another.
- Using Declination Circles: Humans have been using the apparent motion of the Sun as a compass, clock, and calendar for millennia.
- Using Sundials: Humans have been using the Sun’s position to navigate and tell the time, day, and season for millennia. Sundials create shadows that make it easier to do these tasks.

Excellent descriptions, illustrations, models, explanations, applications, so many connections to related subjects and topics.
Wonderful.
Thank you
Thank you, Gunter! I really appreciate that you took the time to explore the website.
Best,
John