Adding Vectors
Adding vectors is a bit more involved than adding scalar quantities (those with only a magnitude) since we can’t add the directions and magnitudes separately. To add vectors precisely, use their axial components. If the vectors are in magnitude and direction form, then calculate their axial components. To quickly estimate the sum of vectors, you may graphically add them in either form: magnitude and direction or axial components. Even when adding vectors mathematically, it is helpful to check your results by adding them graphically since sign errors are quite common in vector addition.
If you are familiar with adding vectors, click one of the buttons to run the app. There is supporting information on adding vectors, running the apps, and additional buttons to run the apps below.
Benefits of Running the Web Apps
Although you can view the following illustrations and animations made using the web apps, running them on your own has several advantages:
-
- The images will be larger.
- You may view any image as long as you like, so you may study and/or draw those that help you most.
- There are additional visualizations and activities to explore.
- Test your understanding by predicting the outcome of new settings before making the change in the app.
- You may save screenshots of visualizations you created.
Suggestion: If you have set your computer screen/computer to sleep at a short time interval, you will lose what you are viewing when running the web app. Consider changing your settings to give yourself time to work with the app as you like.
Adding Vectors Mathematically
To mathematically add vectors, add their corresponding components, then use the Pythagorean Theorem to calculate the magnitude and trigonometry functions to calculate the resultant’s direction.
For example, say you walked 8 miles east (90º) and then 4 miles north (0º) (Figure 1). You are not 8 + 4 or 12 miles or 0 + 90 or 90º from your origin. In this example, each vector is in the direction of one of the axes, so we don’t need to break down the vectors into their component values. We can use the Pythagorean Theorem to calculate how far away we are from where we started and use the inverse tangent to calculate the direction we are from our starting point. See the following sections for details.
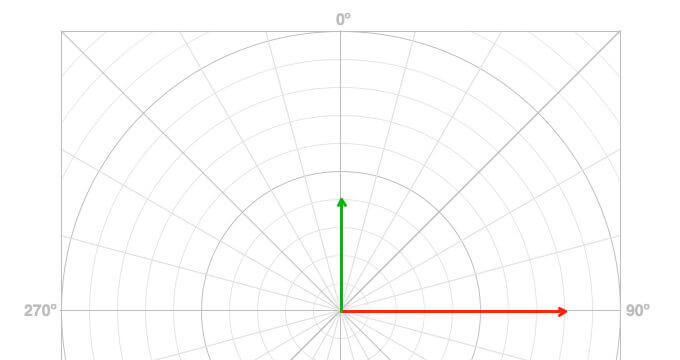
Figure 1: These two vectors are added based on the navigation convention of direction: 0º is north, and the direction increases clockwise. Both vectors are drawn from the origin. Tip: If the vectors are given as magnitude and direction, use a polar grid to plot the vectors from the origin.
Calculate the Resultant’s Magnitude
Using the Pythagorean Theorem:
Magnitude = √(8² + 4²) = 8.9
Calculate the Resultant’s Direction
Direction = 90º – tan¯¹(4/8) = 63.4º (Use Figure 3)
= tan¯¹(8/4) = 63.4º (Use Figure 4)
‘Tail to Tip’ Graphical Addition
“Tail to tip” is the graphical form of vector addition, and it is based on the concept that you can slide the vectors around on the graph. The two solutions, when graphically adding the two vectors shown in Figure 1, are illustrated below. The red vector is 8 miles east (90º), and the green vector is 4 miles north (0º).
In this solution, slide the tail of a second vector to the tip of the first vector. The directions and magnitudes of both vectors remain the same.
If there is a third vector, slide the third vector’s tail to the tip of the sum of the first two vectors.
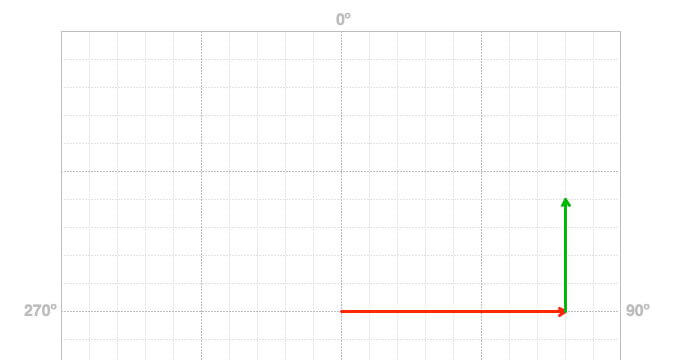
Figure 2: Slide the tail of one vector to the tip of the second vector. Tip: a rectangular grid is useful to plot axial components.
Draw the resultant vector from the origin to the tip of the sum of the two vectors.
When using this technique, create a scale to draw the vectors, so the proportions of the magnitudes are consistent. Draw the vectors’ magnitudes and directions as accurately as possible, so the resultant is conceptually useful and provides a valuable check when mathematically adding the vectors.
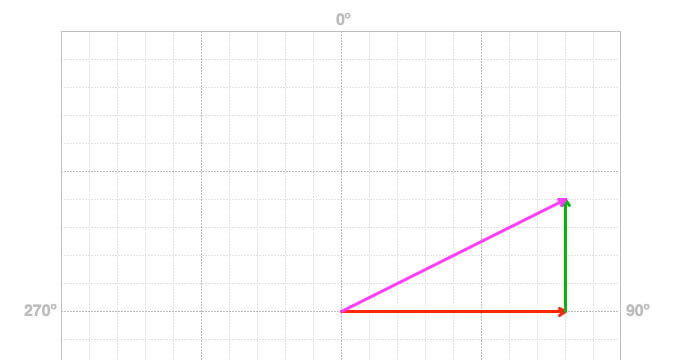
Figure 3: Draw the resultant vector (magenta) from the origin to the tip of the sum of the two vectors.
Does it make a difference which order you add the vectors? In the example above, does it make a difference if you walked east first or north first? Unless there is a fire swamp, Mount Doom, or a whomping willow along one of your paths, you still end up the same distance and direction from where you started. Similar to adding numbers, adding vectors in any order creates the same result.
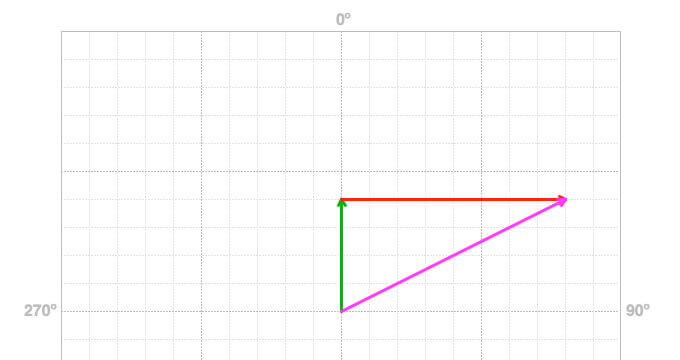
Figure 4: Adding the two vectors in reverse produces the same resultant vector.
Animations of Vector Addition
To help you see how the vectors are repositioned when adding two or three vectors, use the web app, Visually Adding Vectors, to generate random vectors and then move them into a position where the vector tails line up with the tips. Two examples using the app are shown in the following animations.
Click the button to run the web app, Visually Adding Vectors.
Acknowledgments
Many thanks to Brendan Crowley, Alan Gould, Max Hall, and Matti Horne for testing out the app during beta testing.
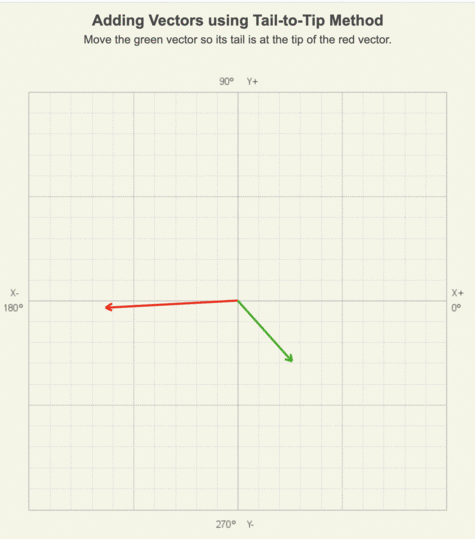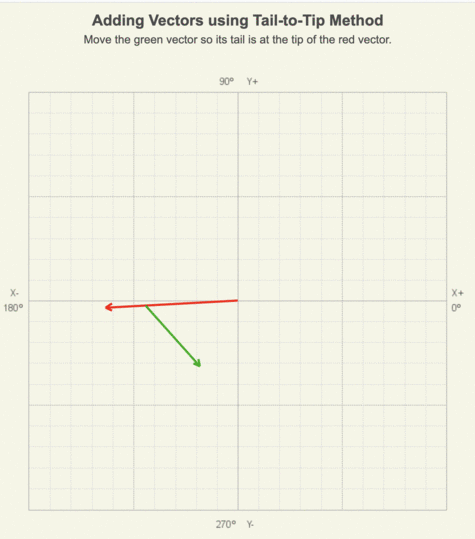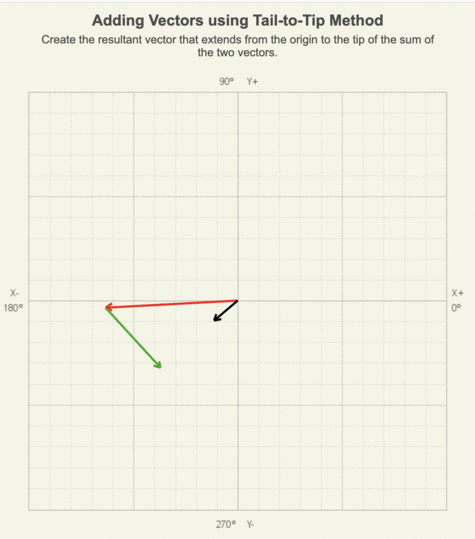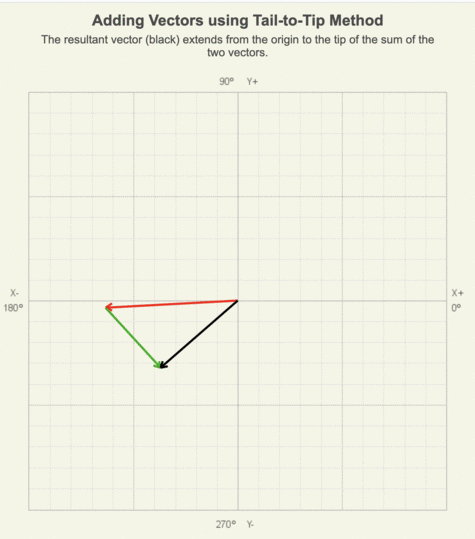
In the animation of adding two vectors using the tail-to-tip method, notice that as the green vector is moved to the red vector’s tip, its length and orientation remain the same.
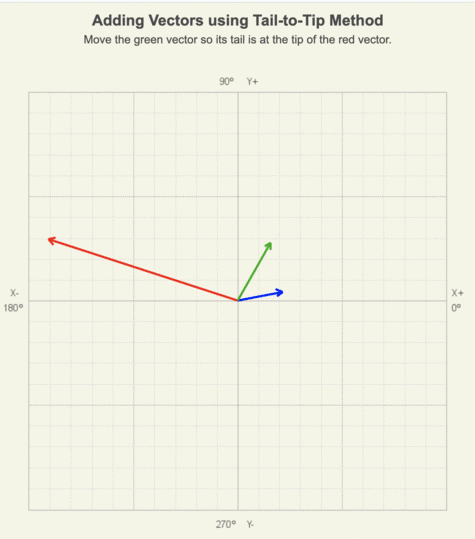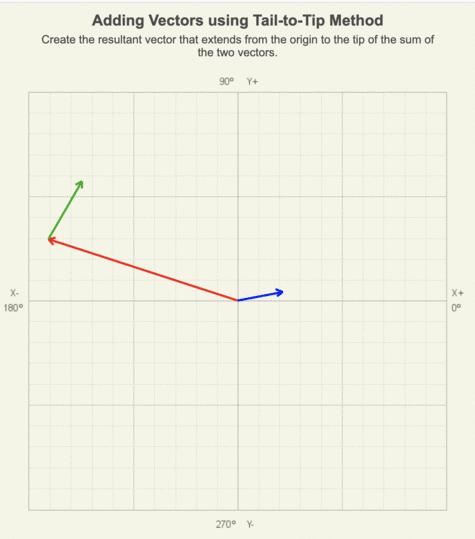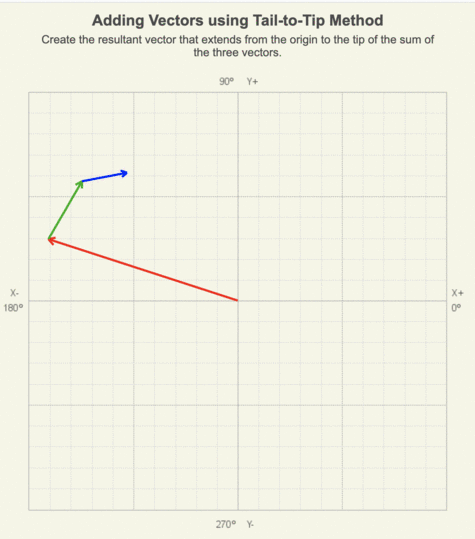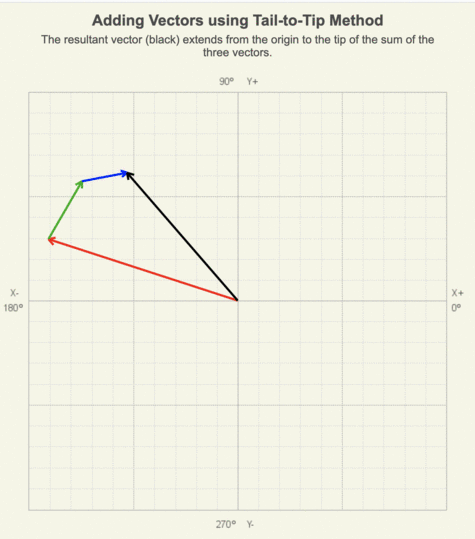
In the animation of adding three vectors using the tail-to-tip method, notice that as the green and blue vectors are moved, their length and orientation remain the same.
Representation and Clarity
There are several ways to graph vector addition. Some may make sense to you; others may be confusing. Is showing the vectors and the resultant vector from the origin clear to you (Figure 5)? This is a common way vectors are displayed when they are to be added.
How is Graphically Adding Vectors Useful?
Working with vectors conceptually is just as important as working with them mathematically. If you are working with vectors mathematically, drawing out the solution catches math errors, especially typos if working with a calculator or computer program and sign errors.
Vectors are used extensively in science, math, and engineering, and mistakes can be more than embarrassing; human lives depend on accurate calculations of built structures, navigation, advanced technologies, weather forecasts, search and rescue, etc.
Most of the remaining sections of Earth Systems require a solid conceptual understanding and application of vectors. Be comfortable with graphically working with vectors.
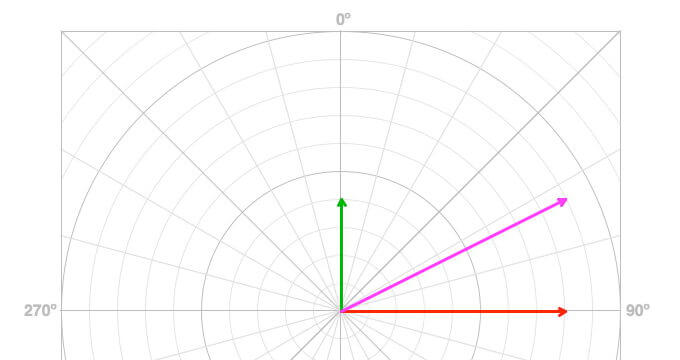
Figure 5: Graph of the vectors being added and the resultant vector from the origin.
How is Mathematically Adding Vectors Useful?
Working with vectors, such as vector addition, is essential in engineering and many branches of science and math. These disciplines would be drastically limited without the use of vectors. Designing and building safe, stable structures (buildings, bridges, roads, dams, etc.) and analyzing and predicting moving objects (airplanes, jets, rockets, etc.), for example, require vector calculations. Highly accurate and precise calculations are essential for a significant part of human technologies.
Adding Three Vectors Mathematically
Conceptually, there is no difference when adding three vectors than when adding two. There is just more to organize.
The following example is when three vectors defined by magnitude and direction are being added.
| Vector | Magnitude | Direction |
| 1 | 4.0 | 45.0º |
| 2 | 8.1 | 310.0º |
| 3 | 6.0 | 180.0º |
Convert the vector’s magnitude and direction to axial components, and then add these to find the resultant’s components.
| Vector | X | Y |
| 1 | 4.0 sin(45) = 2.8 | 4.0 cos(45) = 2.8 |
| 2 | 8.1 sin(310) = -6.2 | 8.1 cos(310) = 5.2 |
| 3 | 6 sin(180) = 0.0 | 6 cos(180) = -6.0 |
| Sum | -3.4 | 2.0 |
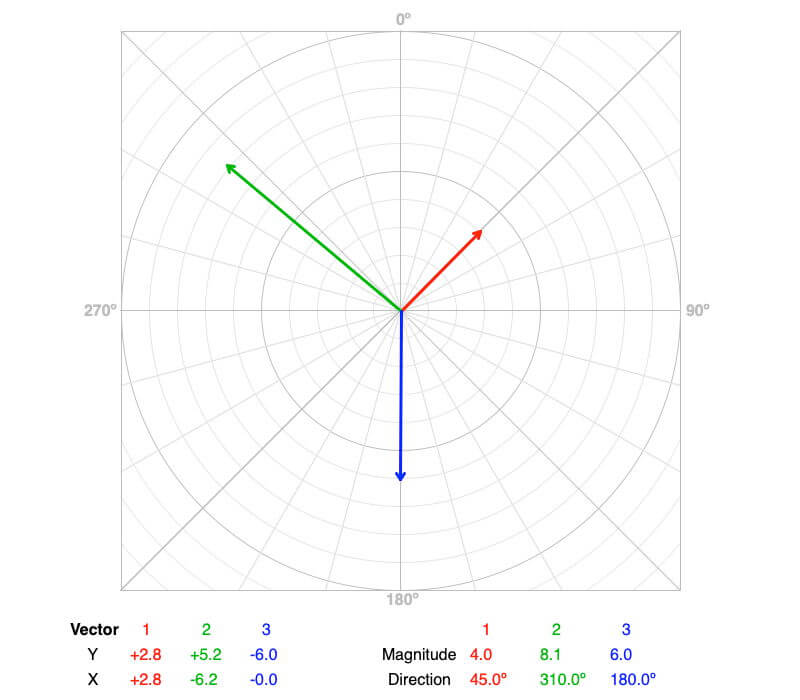
Figure 6: Three vectors to be added. Each vectors’ components are shown. The values are in the same values as their corresponding vector. X represents East when positive, and West when negative. Y represents North when positive, and South when negative.
See Right Triangles and Vectors for details on how vector components are calculated from the magnitude and direction.
Calculate the Resultant’s Magnitude
Using the Pythagorean Theorem:
Magnitude = √(2.0² + (-3.4)²) = 3.9
Calculate the Resultant’s Direction
Direction = 270º + tan¯¹(2.0/3.4) = 300.4º (Use Figure 8)
The difference between this direction and the one shown in Figure 8 is due to round off error using component values limited to tenths compared to using more precise values in the inverse tangent function.
Adding Three Vectors Graphically
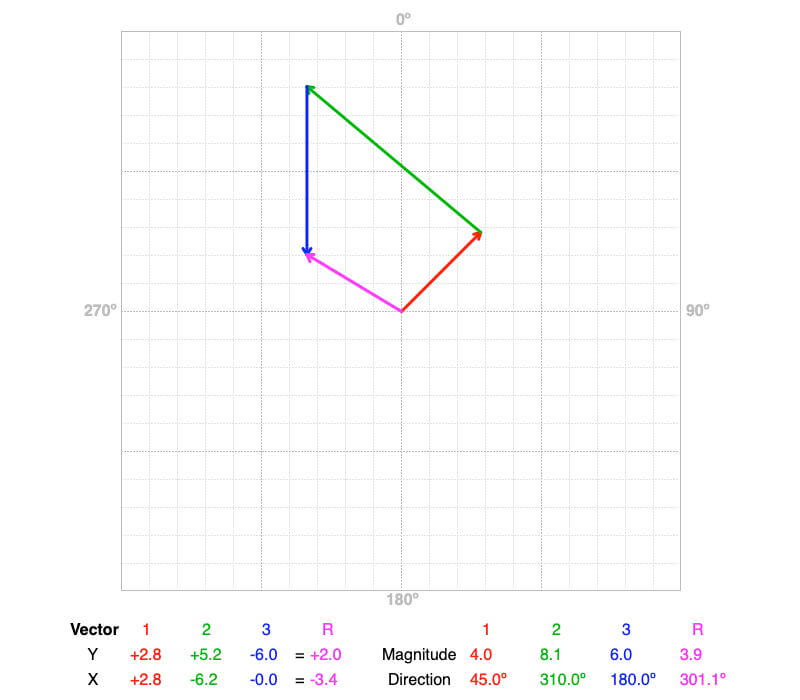
Figure 7: First draw the red vector (vector 1) from the origin, then draw the green vector (vector 2) from the tip of the first, and finally draw the blue vector (vector 3) from the tip of the sum of the first two.
Draw the resultant (magenta) from origin to the tip of the summed vectors.

Figure 8: Add the vectors in another order, the results are the same. There are six possible ways to add the three vectors. Try drawing them on your own.
More Practice?
Click on the button “Adding Vectors web app” for an unlimited number of practice problems adding 2 or 3 vectors graphically or mathematically. Visual and numeric feedback are provided for each problem.
Click the button to run the web app.
The web app uses the trig convention for direction, whereas the examples above use the navigation convention.
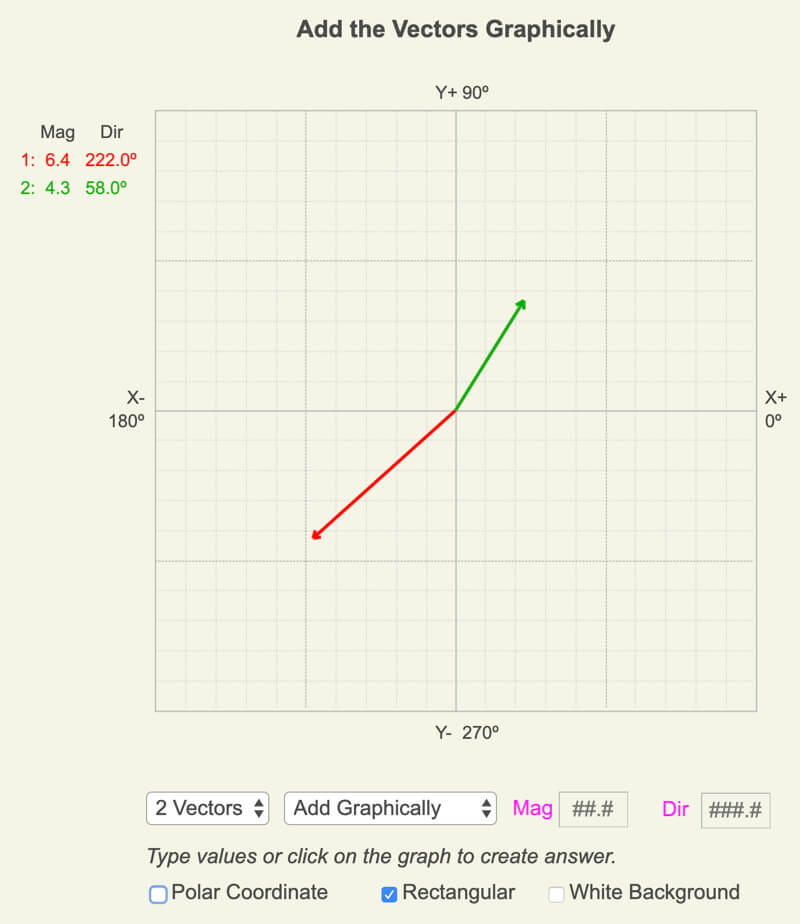
Screenshot of the Adding Vectors web app. When using “Add Graphically,” to create the resultant vector, click on the graph or type the magnitude and direction in the text boxes. When adding mathematically, to meet the needed precision, type the values.

0 Comments