Planet Eccentricity
Eccentricity is the deviation of a planet’s orbit from circularity — the higher the eccentricity, the greater the elliptical orbit. An ellipse has two foci, which are the points inside the ellipse where the sum of the distances from both foci to a point on the ellipse is constant.
Planets orbit massive objects, such as stars, due to the gravitational attraction between the two objects. If the orbit is elliptical, the star is always located at one of the two foci. If the orbit is perfectly circular, the star is in the center of the orbit.
Due to the changing location of the orbiting planets, the gravitational pull between the moving masses is continually changing. These tugs in different directions and magnitudes change the planets’ orbits, including the eccentricity.
In this animation, Earth is at perihelion (closest to the Sun). Notice that the distance between the Sun and Earth decreases considerably as the eccentricity increases. And at aphelion (furthest from the Sun), the distance increases as eccentricity increases.
Note that the sizes of the Sun, Earth, and orbit are not to scale.
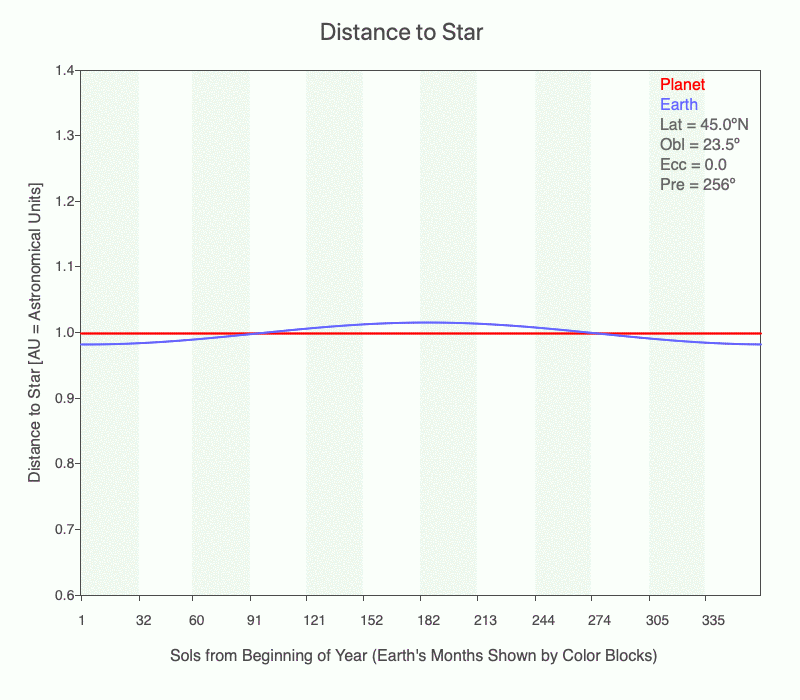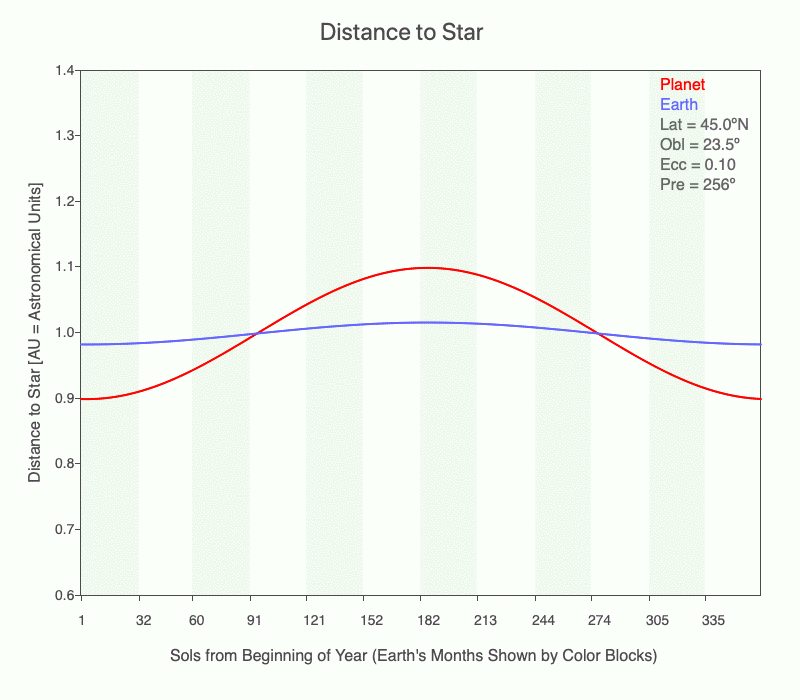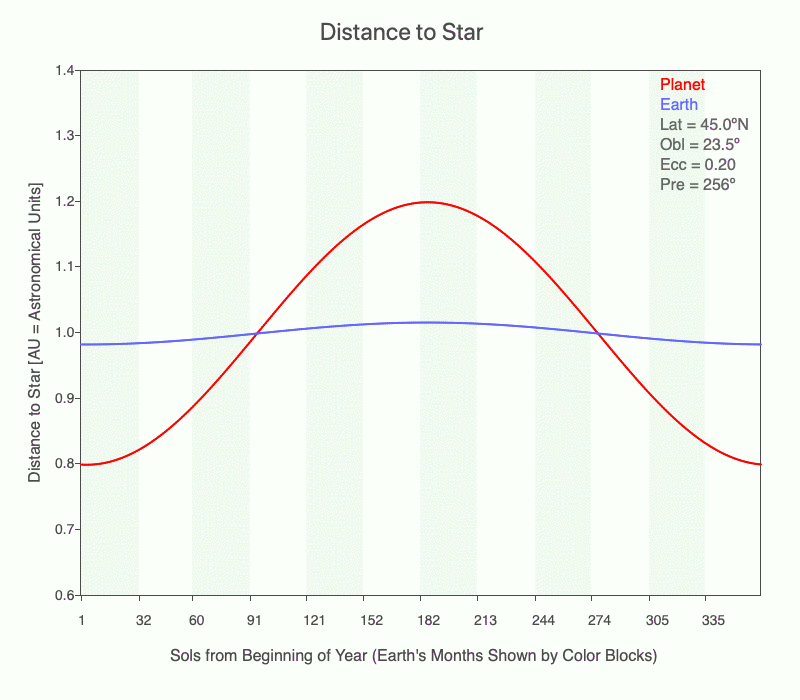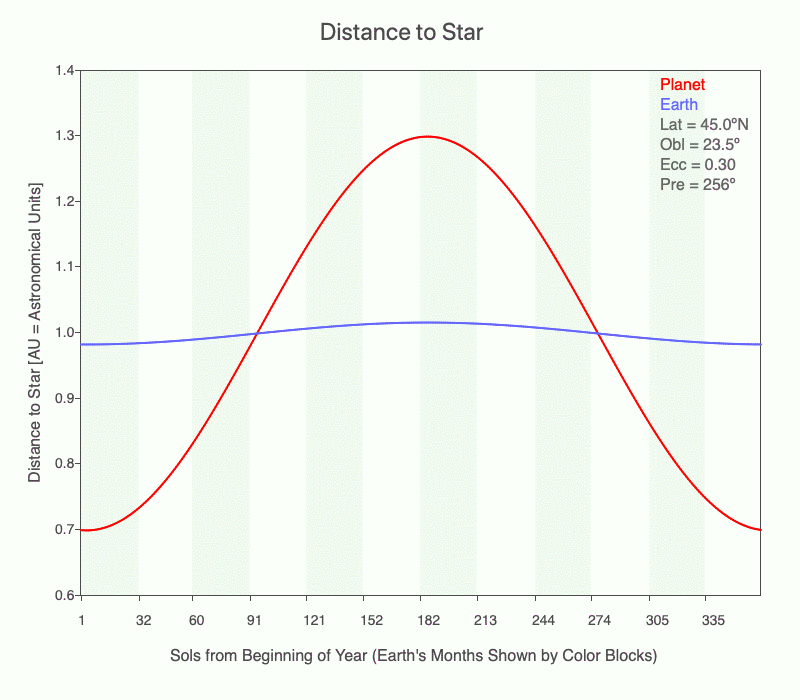
In this animation, the distance between the Sun and Earth changes considerably during an orbit (red line) as the eccentricity increases from 0 to 0.3. Presently Earth’s orbit is slightly elliptical (0.0167), and the distance to the Sun throughout its orbit is shown in blue.
Eccentricity and Duration of Seasons
The magnitude of gravitational attraction depends on the mass of the two objects and the distance between them. The closer the two objects are, the greater the attraction. This increased gravitational pull causes the planet to move faster in its orbit. So when the star and planet are closest, or at perihelion, the planet is moving fastest in its orbit. When furthest away from its sun, or at aphelion, the planet moves the slowest. The season occurring at perihelion is shorter than the season occurring at aphelion. Explore how the durations of the seasons change as Earth’s eccentricity increases from 0 to 0.3 in the following animation.
Earth’s current eccentricity is 0.0167, which creates changes in the lengths of its seasons by several days:
| Duration | NH / SH Season |
| 90 days | Winter / Summer |
| 92 days | Spring / Fall |
| 93 days | Summer / Winter |
| 90 days | Fall / Spring |
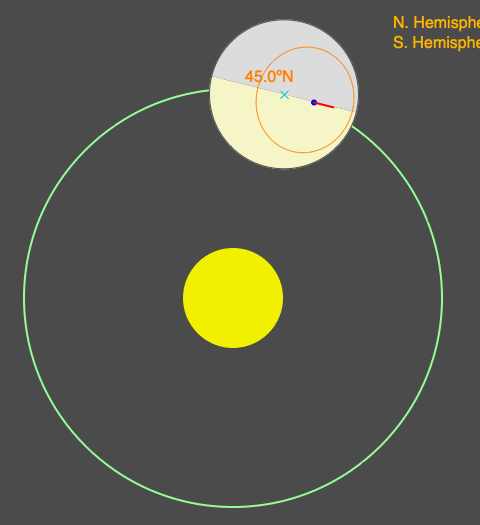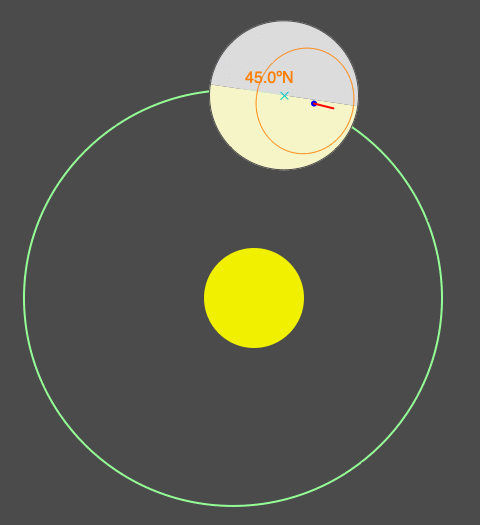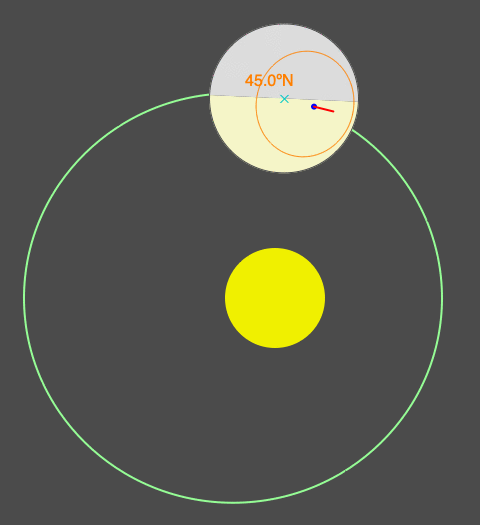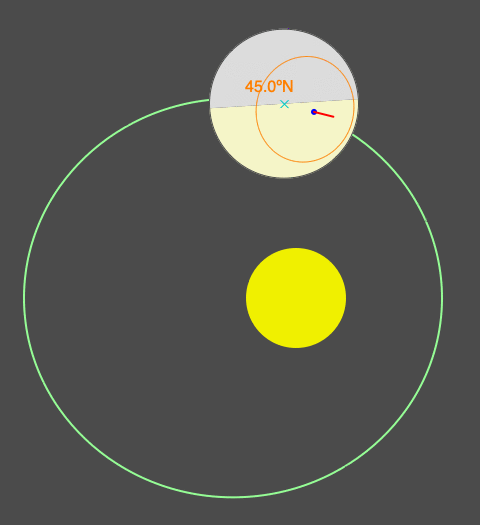
Similar animation as above where eccentricity increases from 0 to 0.03, but now Earth starts are at the Northern Hemisphere spring equinox (so begins spring in the northern latitudes). Notice that as eccentricity increases, more of the Northern Hemisphere is illuminated. The timing and duration of the seasons change as eccentricity changes.
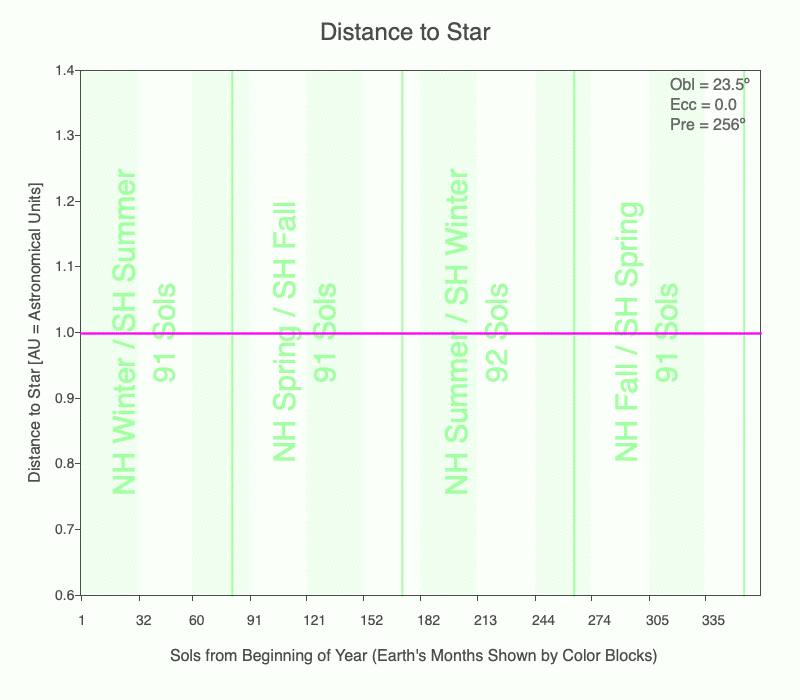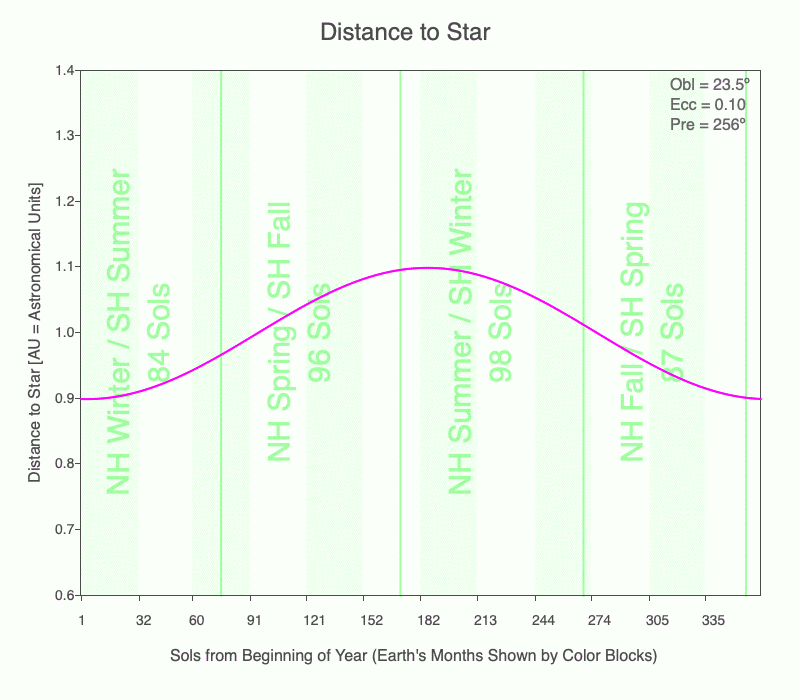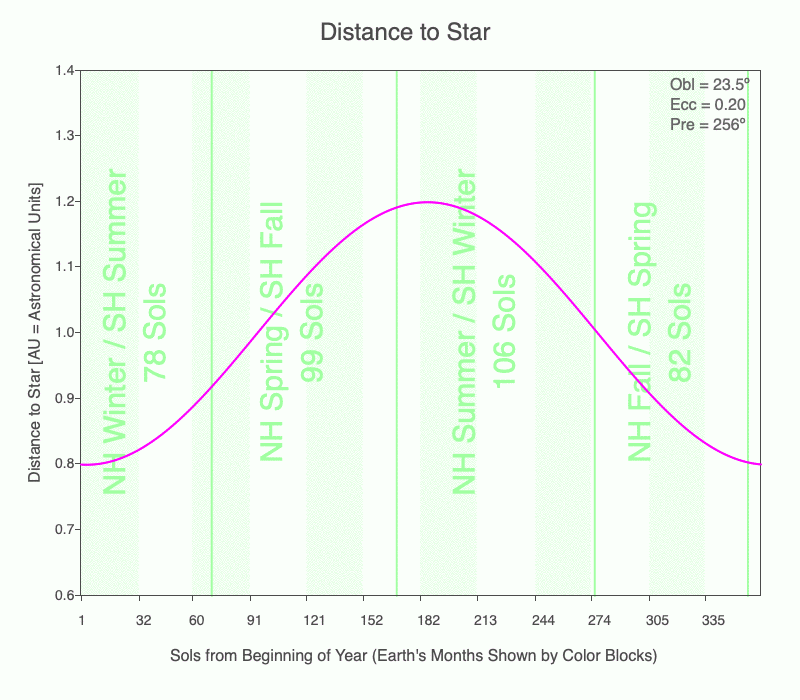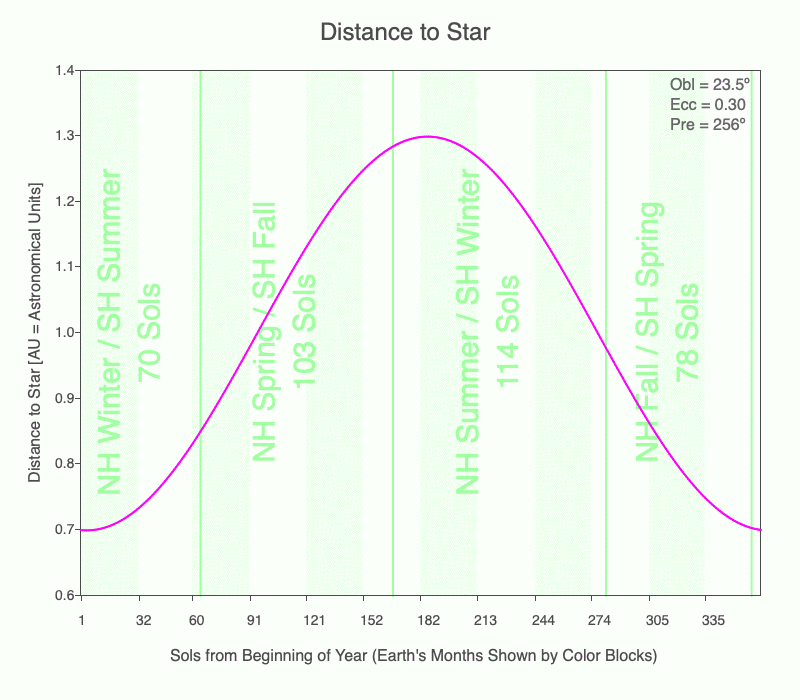
How long each season lasts depends on the eccentricity of the planet’s orbit and when the season occurs relative to perihelion and aphelion. The animation shows the changing lengths of the seasons (vertical green lines) for Earth as its eccentricity changes from 0 to 0.3. The magenta line is the distance between the planet and star that day. 1 AU = average distance between the Earth and the Sun.
Currently, Earth is at perihelion shortly after the Southern Hemisphere (SH) summer solstice, and at aphelion just after the Northern Hemisphere (NH) summer solstice.
Eccentricity and Solar Intensity
As electromagnetic radiation leaves a star, it travels radially outward. So the energy emitted at a given instance in time moves away in an expanding sphere. The sphere’s surface area is 4 π r², so the energy is being distributed over an ever-growing sphere that is proportional to the square of the distance traveled (r²). Since the radiation emitted from a star is generally constant over time, the energy/unit time/unit area decreases at the rate of increase in the surface area of the sphere. For example, an object that is 2r units away from a star receives one quarter the energy compared to the same size object when r units away.
The first frame in the animation of the annual total daily solar energy (TDSE) has an obliquity = 0º and a perfectly circular orbit (eccentricity = 0). There is one season with these conditions since there is no variation in incoming solar radiation. As eccentricity increases, each latitude experiences a change in TDSE, but the equator experiences more than that at 40ºN. Why? When closer to the Sun, the entire planet experiences the same increase in radiation, but since the beam concentration is higher at the equator, there is a higher amount of TDSE.
Even without obliquity creating seasonal temperature change in the midlatitudes and polar regions, large eccentricities (0.1 or higher) create seasonal temperature changes at all latitudes. Luckily, Earth does not have a large enough eccentricity to generate another source of annual temperature change.
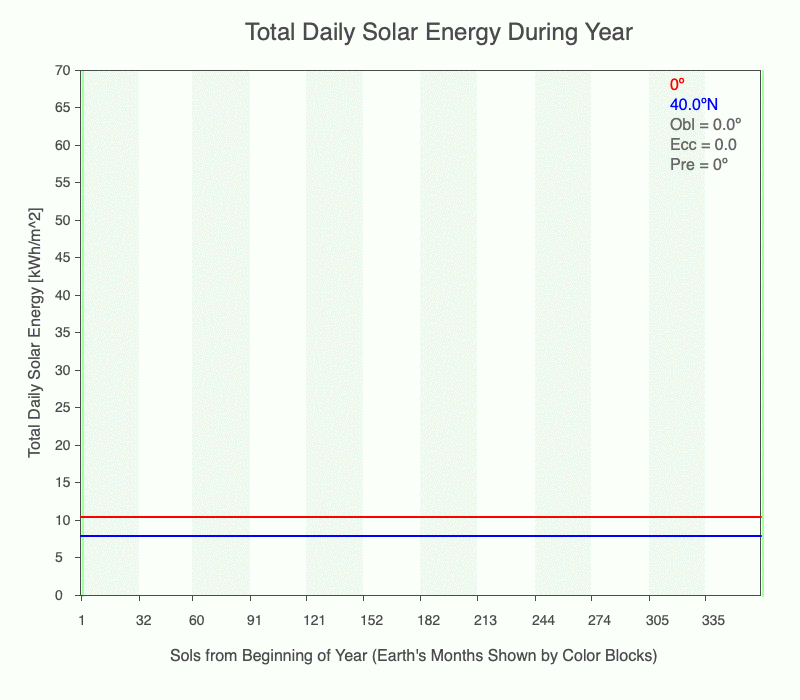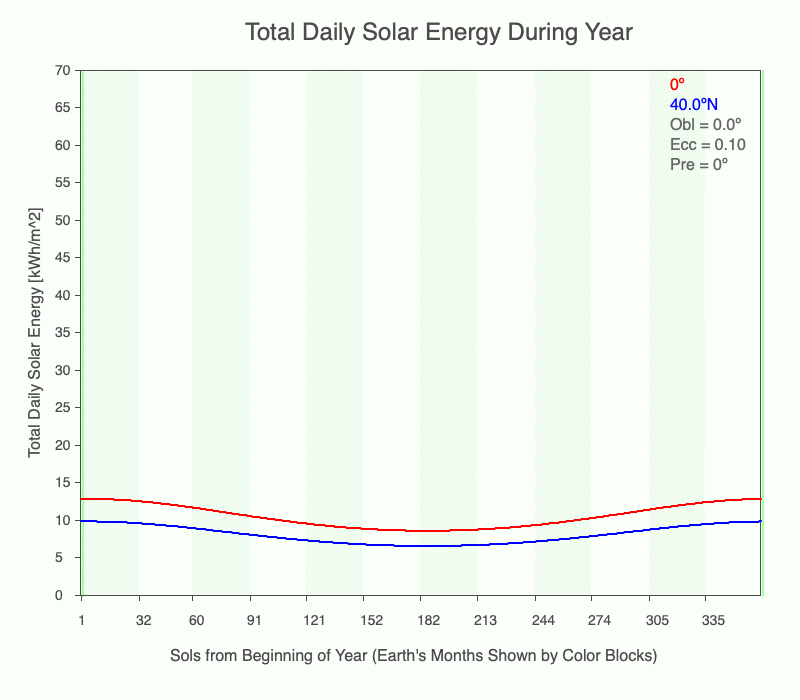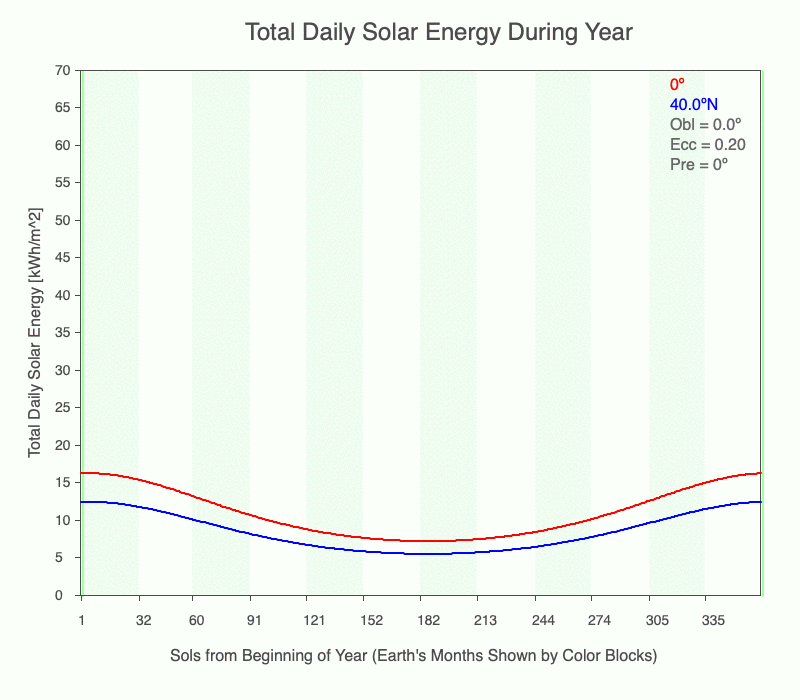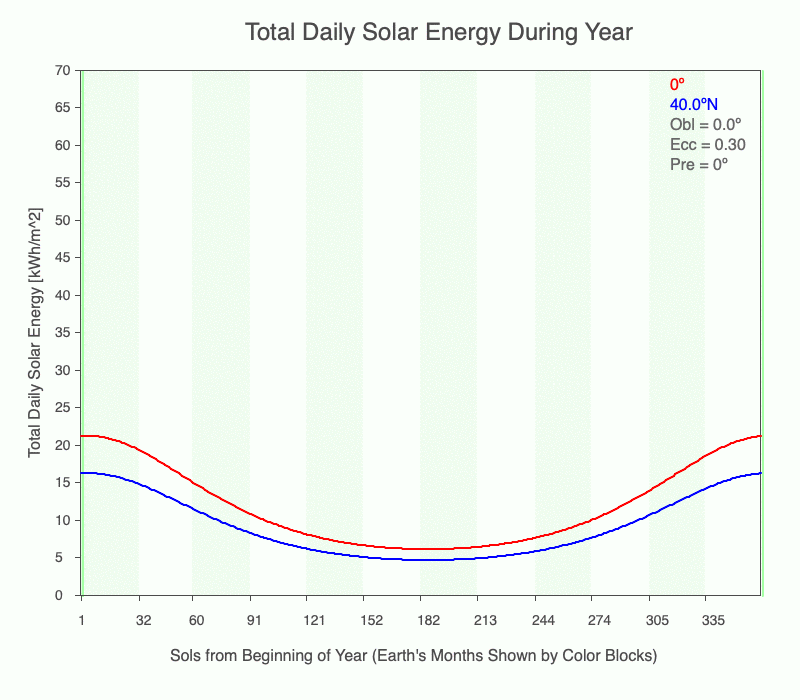
The animation shows the annual change of total daily solar energy at the equator (red) and 40ºN (blue) as its eccentricity changes from 0 to 0.3 and the obliquity is 0º.
Does the Earth’s Radius Have an Effect on Solar Radiation?
On average, Earth is 93 million miles from the Sun, and Earth’s radius is almost 4000 miles. Does this difference in the distance affect the intensity of sunlight reaching the Earth’s surface?
Let’s take a look at the percent difference from the closest point on Earth to the Sun to the illuminated point that is furthest from the Sun:
(93×10^6 – 4000) / (93×10^6) = 99.9957%
This closest point on Earth to the Sun would experience 1.000086 times more radiation than the furthest illuminated point. This will have a negligible effect compared to the changing beam concentration with latitude.
Summary
As orbits become more elliptical, the range of distance between the planet and its star increases. The changing distances have two effects:
-
- Speed up and slow down parts of the planet’s orbit, which changes the timing and duration of the seasons.
- Change the intensity of the sunlight reaching the planet. The closer the planet is to the star, the more intense illumination. Eccentricities ≥ 0.1 create noticeably hotter and colder seasons for all latitudes. The latitudes experiencing the greatest seasonal temperature change depend on the solar declination during aphelion and perihelion.
Continue Exploring the Impacts of Eccentricity on a Planet’s Radiation Budget
Use the desktop app, Star-Planet Connection, to explore the planet’s illumination at any day during its orbit as you change eccentricity. Download Mac or PC versions at the Software page.
Big Ideas
- Eccentricity is the deviation of a planet’s orbit from circularity — the higher the eccentricity, the greater the elliptical orbit.
- An ellipse has two foci: the points inside the ellipse where the sum of the distances from both foci to a point on the ellipse is constant.
- If the orbit is elliptical, the star is always located at one of the two foci. If the orbit is perfectly circular, the star is in the center of the orbit.
- Because gravitational pull between the planet and star increases as the distance between the two decreases, the planet moves fastest in its orbit when closest to the star, and slowest when furthest away.
- The changing orbital speed changes the duration of a planet’s seasons.
- For considerably elliptical orbits, the star’s radiation reaching the planet may vary considerably between its orbit’s closest and furthest points.

0 Comments