Wind and Balanced Forces
The goal of this Earth, Wind, and Forces section is that you will be able to draw the general wind pattern given a map of air pressure, whether you are in the Northern or Southern Hemisphere, and how rough the Earth’s surface is at this location. You aren’t expected to be precise, but instead, you should understand and apply how four forces (pressure gradient force, friction, Coriolis force, and centrifugal force) create and guide the wind on our planet.
Winds and Forces
We will explore this section as most Physics courses explore the motion of objects. First, analyze the kinematics of the moving object: how things move. Then study the dynamics of the moving object: why things move. This makes it easier to focus on the patterns of wind first, and then on the conditions affecting the forces acting on the moving air.
Winds and Unbalanced Forces
Before we talk about wind and balanced forces, we need to explore how air started to move in the first place. This means we need to examine winds and unbalanced forces.
Straight Isobars
Straight isobars produce winds that don’t curve, so centrifugal force is negligible. We only focus on three forces: pressure gradient force, Coriolis force, and friction. Since Coriolis force and friction are both zero for still air, the only force that gets air to move is the pressure gradient force.
These animations illustrate how still air at 45ºN responds to a north-pointing pressure gradient of 4 mb / 100 km. The drag coefficient, which reflects the roughness of the surface interacting with the wind, is representative of a forest.

What patterns do you observe as the wind starts to blow until it becomes balanced?
1) The still air accelerates most in the first increment of time (iteration), and it is in the direction of the pressure gradient. Each following time increment, the wind speed increase less.
2) With each iteration, the wind moves further to the right of the pressure gradient, although the amount to the right decreases after the fourth iteration.
3) Eventually, the change in wind speed and direction become negligible. There is a slight decrease in wind speed during the final iterations.
Data: (Direction = Dir, Δ = Change)
| Iteration | Speed | ΔSpeed | Dir | ΔDir |
| 0 | 0.0 | 0.0º | ||
| 1 | 4.3 | 4.3 | 0.0º | 0.0º |
| 2 | 8.3 | 4.0 | 3.7º | 3.7º |
| 3 | 11.5 | 3.2 | 7.4º | 3.7º |
| 4 | 13.6 | 2.1 | 11.1º | 3.7º |
| 5 | 14.7 | 1.1 | 14.4º | 3.3º |
| 6 | 15.3 | 0.6 | 17.2º | 2.8º |
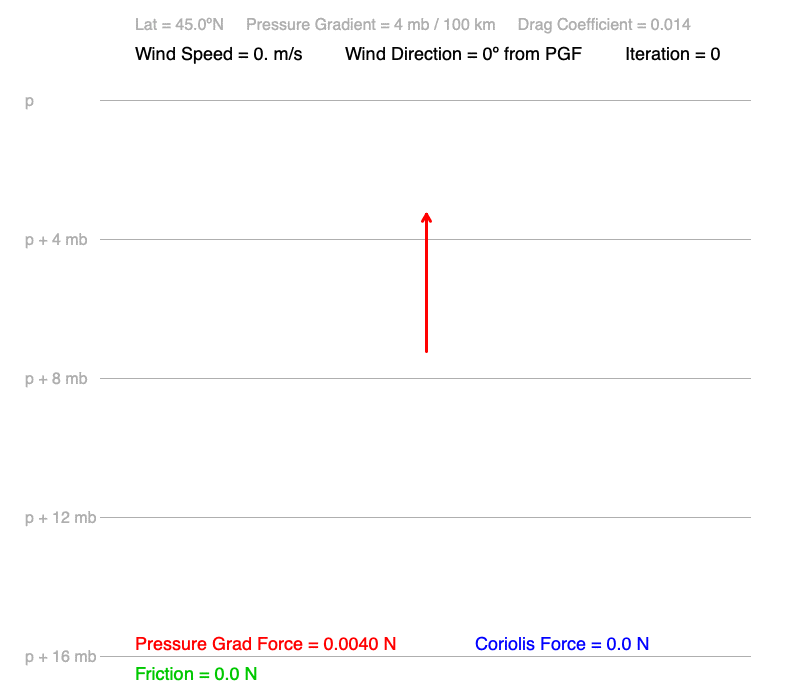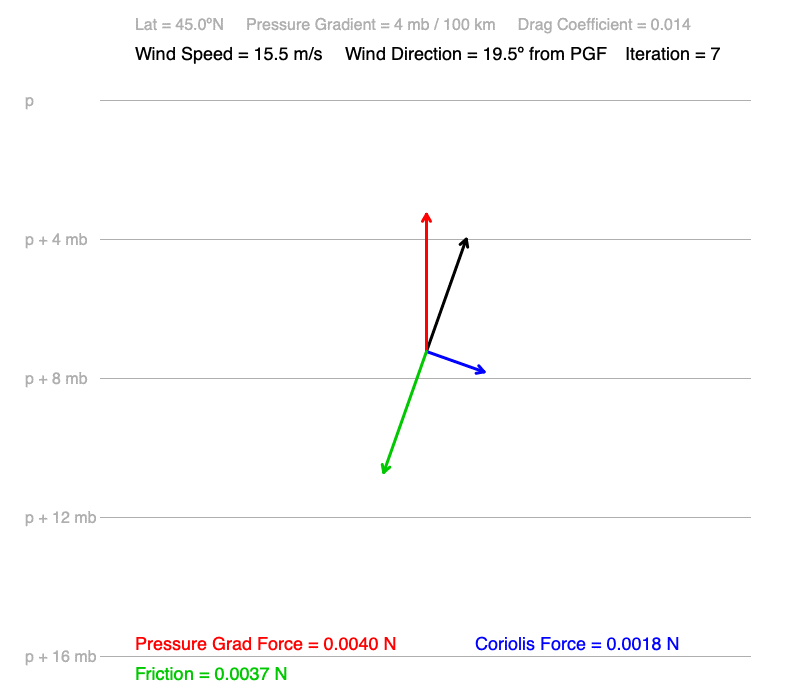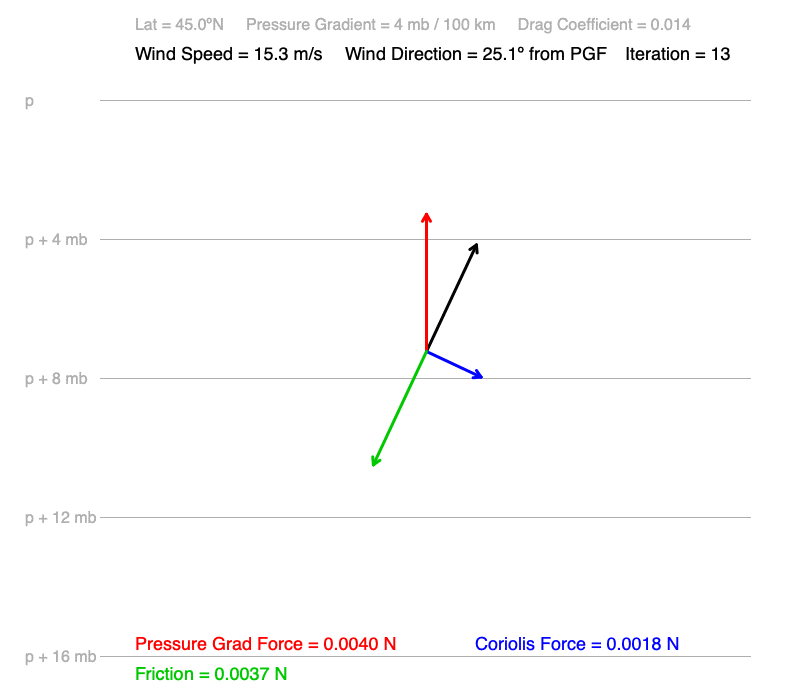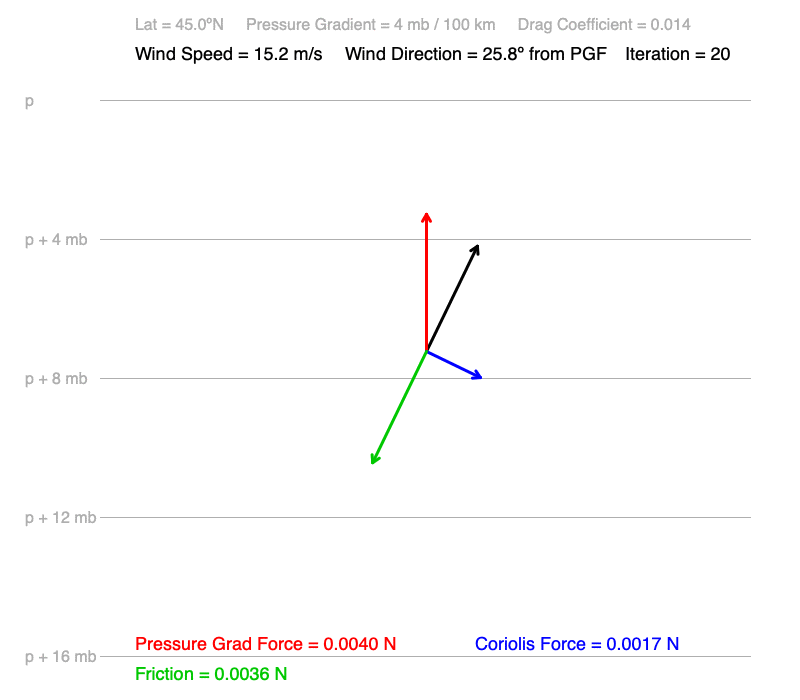
| 7 | 15.5 | 0.2 | 19.5º | 2.3º |
| 8 | 15.5 | 0.0 | 21.3º | 1.8º |
What cause these patterns?
1 & 2) Since only pressure gradient force is acting on the still air, it accelerates in the direction of the pressure gradient. As soon as the air is moving, Coriolis force and friction begin to act on the air. Both forces are proportional to the wind speed: the faster the wind, the greater the friction and Coriolis acting on the moving air.
The Coriolis force is always perpendicular to the wind direction. Since we are in the Northern Hemisphere, the Coriolis force pushes the wind to the right of its motion. The more the wind veers away from the pressure gradient, the less push it experiences from the pressure gradient.
Friction always opposes the motion of the wind. As the wind speed increases in the early iterations, friction offsets a portion of gains in speed.
3) Notice that as the change in wind speed and direction slows, the orientations and magnitudes of friction and Coriolis force change very little. The three forces acting on the wind are coming into balance. The small increase in friction just before the forces become balanced decrease the wind speed slightly.
Winds with Balanced Forces
Since most wind generally has balanced forces, we will focus on these conditions.
The angle the winds cross the isobars is called the cross-isobar angle. When the wind is perpendicular to the isobars (so parallel to the pressure gradient), the cross-isobar angle is 90º. When the wind is parallel to the isobars (and perpendicular to the pressure gradient, the cross-isobar angle is 0º.

An example of a cross isobar angle used to show the wind’s direction relative to the isobars. Isobars are lines of constant air pressure. The wind vector is black, and the isobars are gray.
Effect of Coriolis Force (Latitude)
In the following animations, latitude begins at the North Pole (90ºN) and moves south 5º each frame. The pressure gradient is 7 mb / 100 km (which is quite strong) and points northward. The drag coefficient, which reflects the roughness of the surface interacting with the wind, is representative of a forest.

What patterns do you observe as latitude changes?
1) The cross-isobar angle increases going toward the Equator (0º), so the air flows closer to the direction of the pressure gradient.
2) Wind speed increases approaching the Equator (0º).
3) Winds move to the right of the pressure gradient north of the Equator and the left south of it. Remember, the pressure gradient is perpendicular to the isobars.
4) The change in wind direction decreases going to the poles (90º). The largest deflection under these conditions is 27.6º, which occurs at the North and South Poles.
5) Something odd is happening at the Equator (0º). Winds are at an unrealistic speed – over 1300 mph!
6) Wind speeds and the amount of deflection of the wind from the pressure gradient are the same at corresponding latitudes in each hemisphere. For example, 30ºN and 30ºS each have wind speeds of 20.9 m/s and the wind is 14.0º away from the pressure gradient (to the right at30ºN and the left at 30ºS).
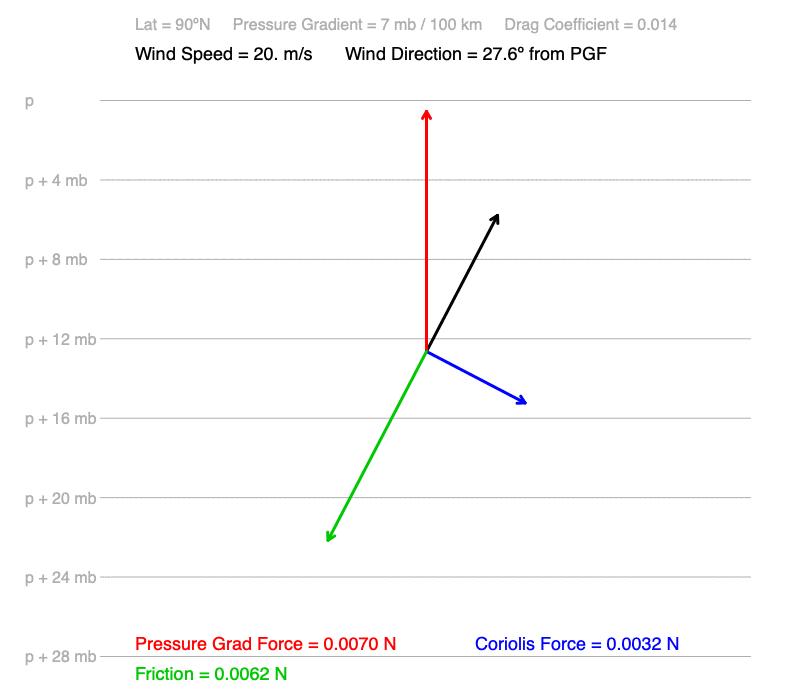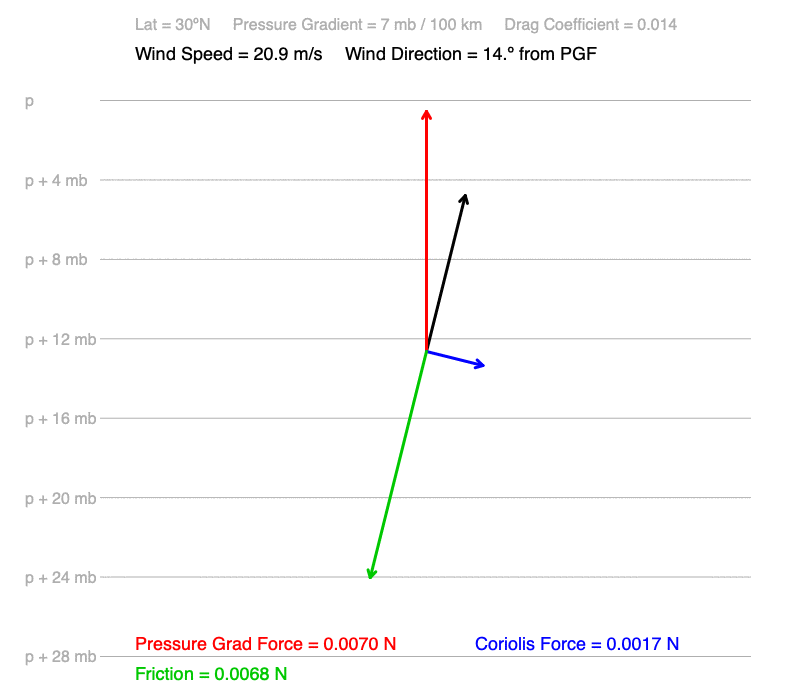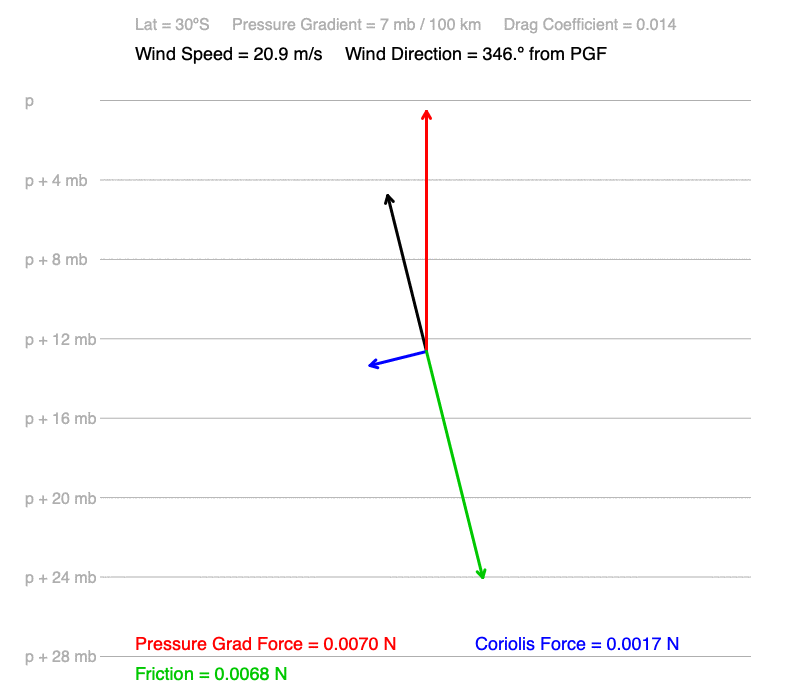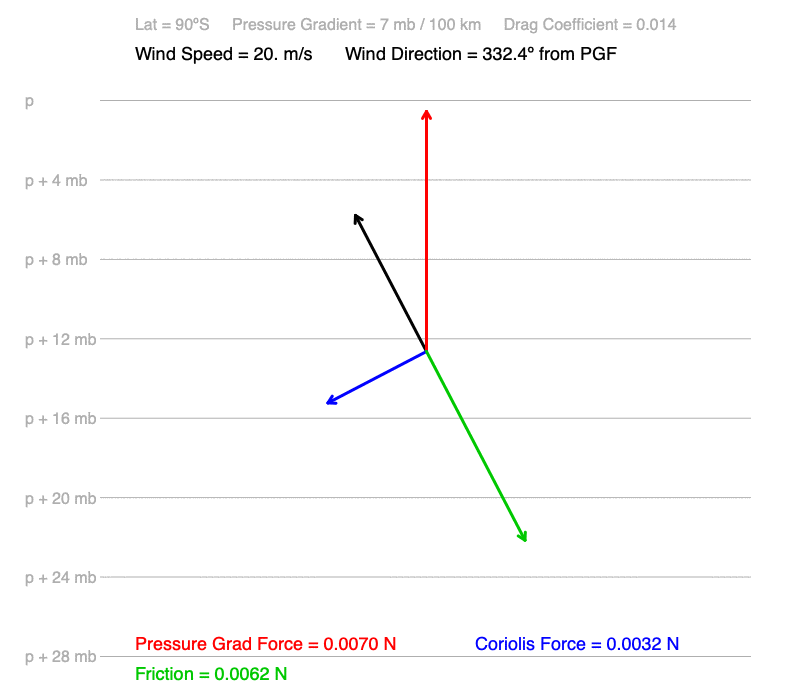
What cause these patterns?
1) The cross-isobar angle increases going toward the Equator (0º) since the amount of deflection by the Coriolis force decreases toward the Equator. At the Equator, the Coriolis force is zero on all moving air, not just still air.
2) Wind speed increases approaching the Equator (0º) since the wind remains moving in a direction similar to the pressure gradient. The pressure gradient is the force that increases wind speed. The longer the wind is moving in a similar direction, the greater amount of time to accelerate its speed before the forces acting on the moving air become balanced.
3) Winds move to the right of the pressure gradient north of the Equator and the left south of it. The Coriolis force acts perpendicular to the right of moving air in the Northern Hemisphere, and to the left in the Southern Hemisphere.
4) The change in wind direction decreases going to the poles (90º). Although the Coriolis force is at its maximum at the poles, it doesn’t change much with small changes in latitude. Toward the Equator, however, Coriolis force, which is calculated using the Coriolis coefficient, changes quite a bit with small changes in latitude (see the graph below).
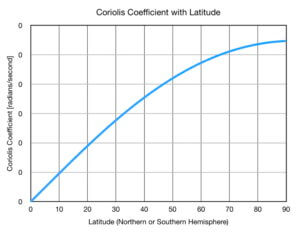
5) Something odd is happening at the Equator (0º). Winds are at an unrealistic speed – over 1300 mph! Since the Coriolis force is zero, there are only two forces acting on the wind at the Equator: pressure gradient force and friction. Since friction is proportional to wind speed, the wind must be quite fast to offset the acceleration that has occurred in the direction of the pressure gradient.
6) Wind speeds and the amount of deflection of the wind from the pressure gradient are the same at corresponding latitudes in each hemisphere. For example, 30ºN and 30ºS each have wind speeds of 20.9 m/s and the wind is 14.0º away from the pressure gradient (to the right at30ºN and the left at 30ºS).
Effect of Pressure Gradient
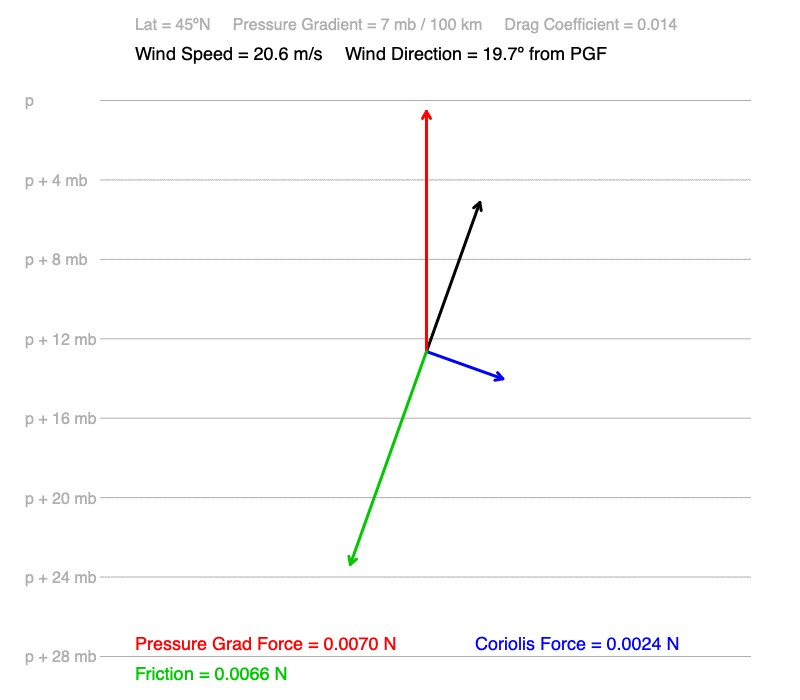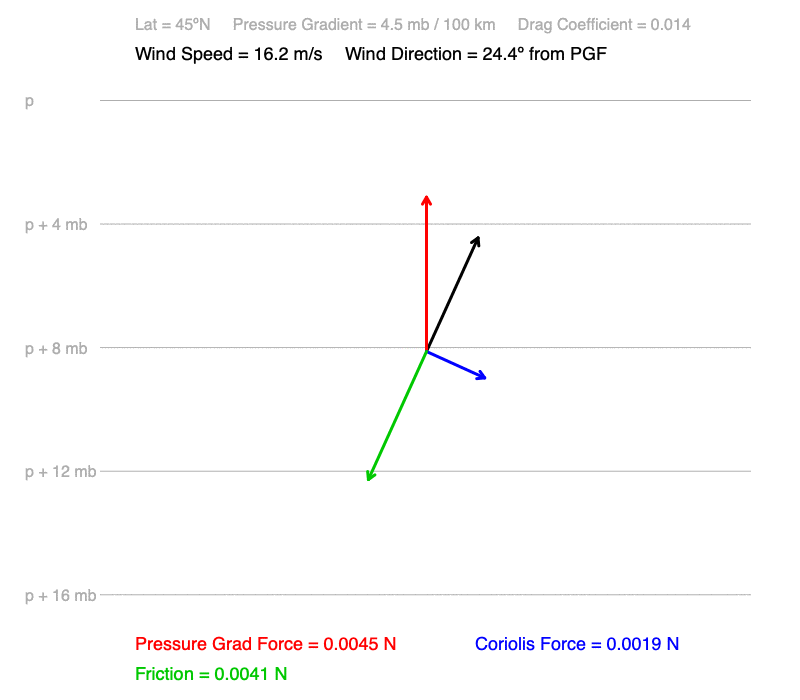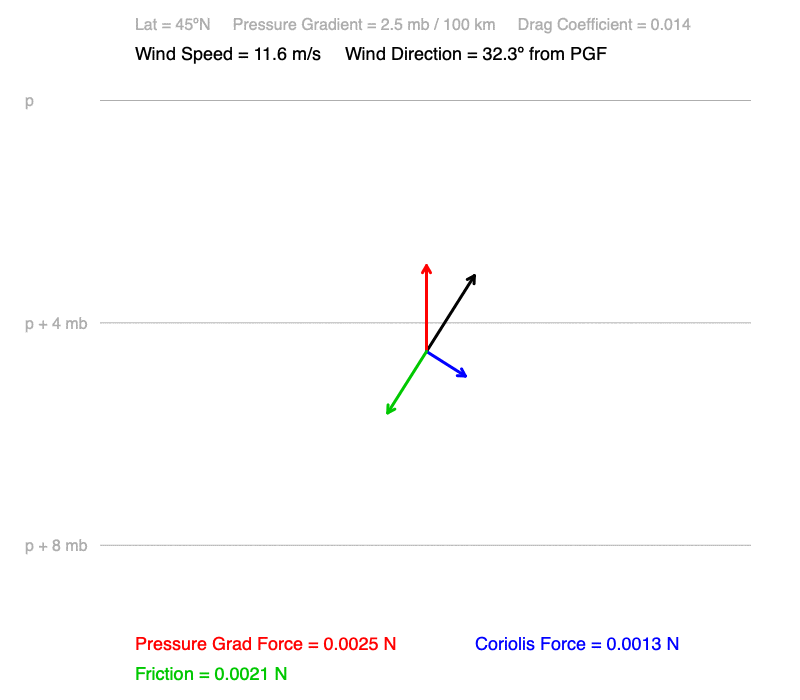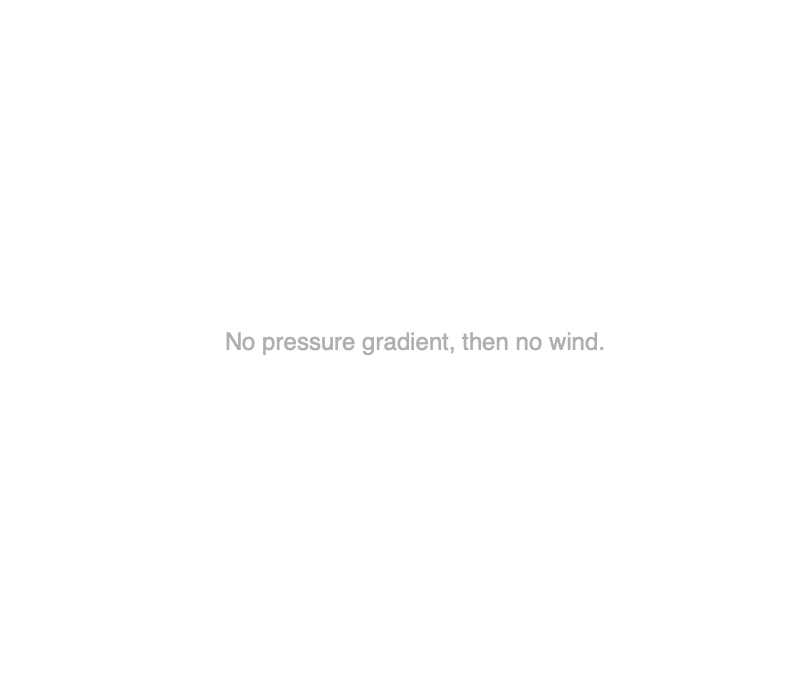
In these animations, the north-pointing pressure gradient decreases from 7 to 0 mb / 100 km. The drag coefficient which is representative of the roughness of a forest acting on the wind. The latitude is 45ºN.

What patterns do you observe as pressure gradient decreases??
As the pressure gradient decreases:
1) Wind speed decreases, and
2) The cross-isobar angle decreases. The wind turns away from the pressure gradient, which is perpendicular to the isobars.
What cause these patterns?
1) The pressure gradient is the amount of push acting on air to make it accelerate. The higher the pressure gradient, the greater the acceleration, and the higher the wind speed.
2) The two forces that are proportional to the wind speed, friction and Coriolis force, increase at different rates as wind speed increases. At low wind speeds, the magnitude of the Coriolis force is greater than that of friction, so the wind turns away from the direction of the pressure gradient. At higher wind speeds, the magnitude of friction is greater than the Coriolis force, resulting in a wind direction closer to the direction of the pressure gradient.
Effect of Friction (Drag Coefficient)
In these animations, the drag coefficient, which characterizes the roughness of the surface interacting with the wind) decreases from 0.03 (a heavily forested mountain) to 0 (no friction). The pressure gradient is 7 mb / 100 km, and the latitude is 45ºN.

What patterns do you observe as friction decreases?
As friction decreases:
1) The wind speed increases, and
2) The cross-isobar angle decreases. When friction is zero, the wind is parallel to the isobars.
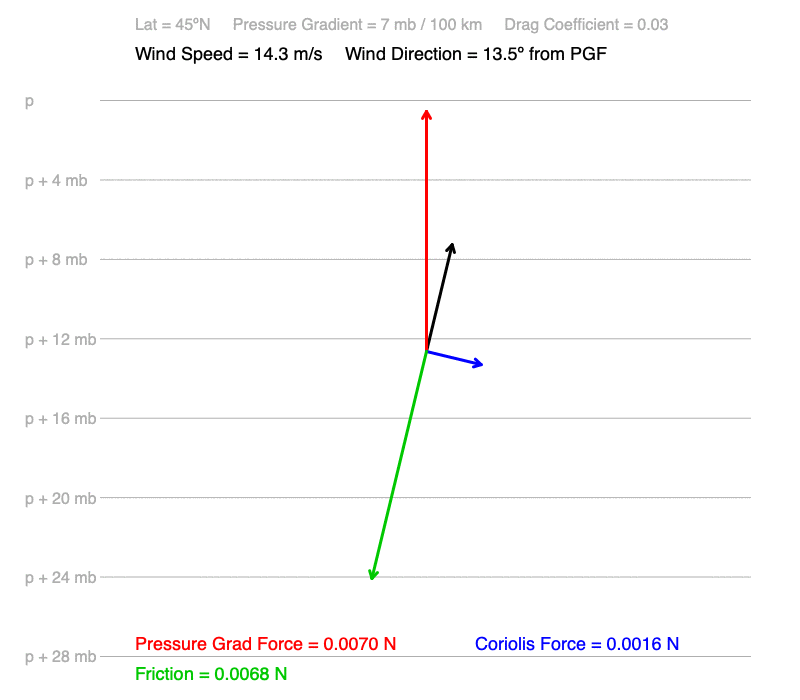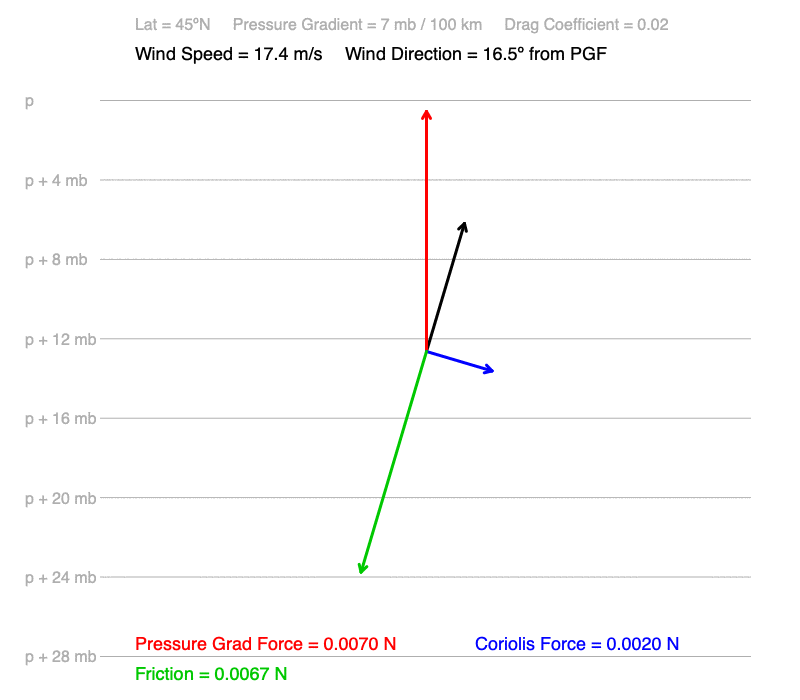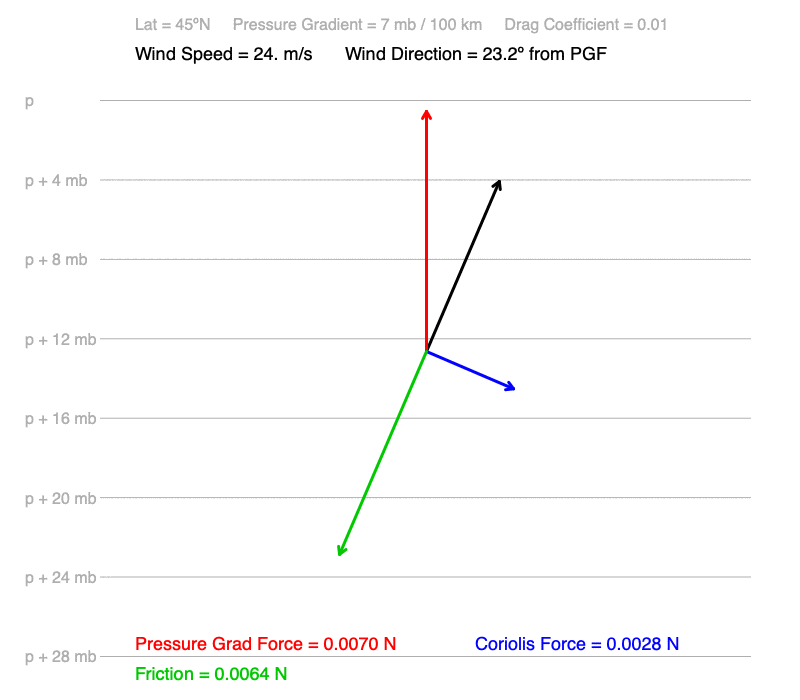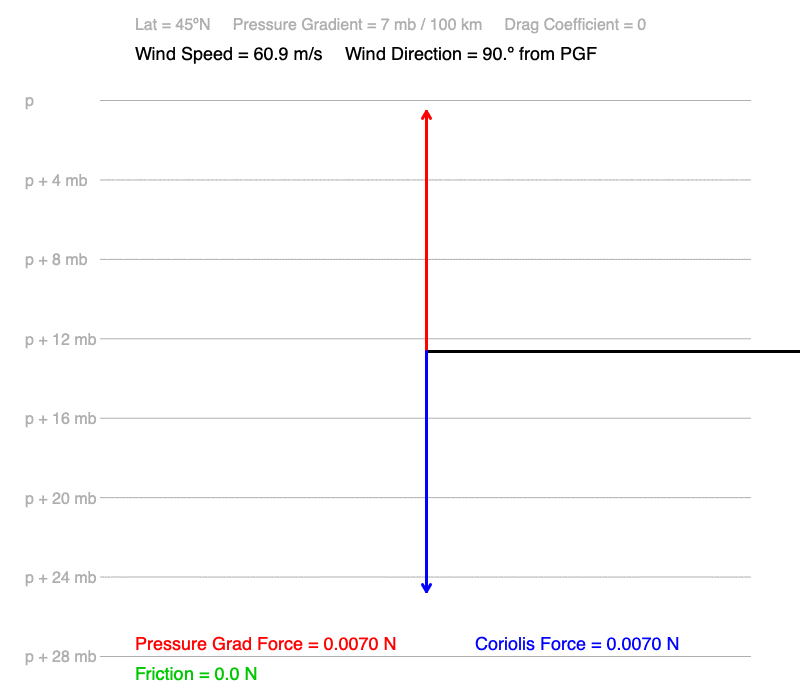
What cause these patterns?
1) Since friction opposes the motion of the wind, when there is less friction, there is more acceleration by the pressure gradient.
2) When friction is zero, the Coriolis force must balance the pressure gradient force. The wind stops accelerating when the Coriolis force is equal and opposite the pressure gradient force. Since Coriolis is always perpendicular to the wind, the wind is parallel to the isobars.
Wind calculations are based on Roland Stull’s online book “Practical Meteorology: An Algebra-based Survey of Atmospheric Science“, in particular, Chapter 10 “Atmospheric Forces and Wind.” This book is an invaluable resource for those wanting to dive into the mathematical analysis of atmospheric phenomena.
Wind Challenges
Test your understanding by drawing the forces acting on each of the challenges below.
You aren’t expected to know the magnitudes of any of the forces, but you should be able to draw reasonable magnitudes and directions.
Northern Hemisphere surface wind
Pressure gradient exists since the wind is moving.
Friction exists because the wind is at the surface. Friction always opposes the motion of the air, so it points toward the west.
Coriolis force exists since the air is moving in the Northern Hemisphere. Coriolis force is always perpendicular to the wind’s direction, so since in the Northern Hemisphere, Coriolis points to the right of the wind direction.
Depending on the magnitudes for friction (green) and Coriolis (blue), draw the pressure gradient force (red) so it creates a balanced set of forces.
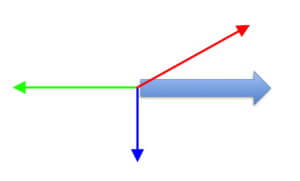
Southern Hemisphere 200 mb wind
Pressure gradient exists since the wind is moving.
Friction does NOT exist because the wind is well above the surface. One atmosphere is just a bit more than 1000 mb, and this wind is at 200 mb, so 80% of the atmosphere is below it.
Coriolis force exists since the air is moving in the Southern Hemisphere. Coriolis force is always perpendicular to the wind’s direction, so since in the Southern Hemisphere, Coriolis points to the left of the wind direction.
To create balanced forces, the pressure gradient force (red) is equal but opposite the Coriolis force (blue).
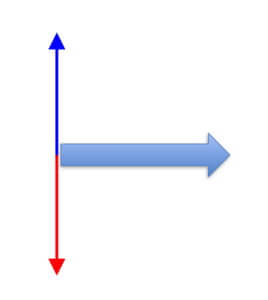

Draw the balanced forces acting on a 10 mph west wind for the following challenges.
Surface wind at the Equator
Pressure gradient exists since the wind is moving.
Friction exists because the wind is at the surface. Friction always opposes the motion of the air, so it points toward the west.
Coriolis force does NOT exist at the Equator
To create balanced forces, the pressure gradient (red) must be equal but opposite the friction (green).
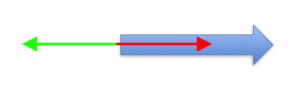
200 mb wind at the Equator
Pressure gradient exists since the wind is moving.
Friction does NOT exist since the air is well above the ground. One atmosphere creates a surface air pressure of roughly 1000 mb. At 200 mb, 80% of the atmosphere is beneath this wind’s altitude.
Coriolis force does NOT exist at the Equator.
Since there is one force acting on the air, it CANNOT be balanced, so this wind does not exist in these conditions.
Continue to Explore Winds
Use the desktop app, Earth, Wind, and Forces, to explore winds on Earth. Go to the Software page to download a version for Macs or PCs.

0 Comments