Vectors and the Laws of Motion
Energy has the ability to make things move, but forces are what get things to speed up, slow down, and change direction. A force is the amount of push or pull acting on an object, so it is a vector. The amount of push/pull is the magnitude, and the push or pull indicates the direction.
If you are familiar with the concept of balanced forces, click the button to run the web app. There is supporting information about balanced forces, how to run the app, and a second button to run it below.

Balanced forces: the rock is not moving since the ground is pushing back equally against its weight. Since the rock is not moving, it will stay that way when the forces acting on it are balanced.
Newton’s Laws of Motion
Isaac Newton identified three key relationships (or laws) about forces and motion:
1) The acceleration of an object is equal to the force acting on an object divided by the mass of the object, or rewritten as F = ma
-
- The position is where something is located, and in this case, it is defined as x.
- Displacement is the change in position of an object: △x = x1 – x0
- Velocity is the rate that displacement is changing: v = △x / △t = (x1 – x0) / (t1 – t0)
- Acceleration is the rate that the velocity is changing: a = △v / △t = (v1 – v0) / (t1 – t0)
All three variables, plus force, are vectors.
An object accelerates when it changes speed or when it changes direction. The lit metal fragments of the sparkler move in a circle when they are attached to the sparkler, but once they leave it, they move in a straight line.
2) A body accelerates when acted upon by an unbalanced force.
If only one force acts on a body, it is unbalanced, and the object accelerates in the direction of the single force.
If two or more forces acting on an object add to zero, they are balanced, and there won’t be a change in motion (direction or speed). For example, if the object moves in a straight line, it will continue to move in the same direction and speed. If the body is at rest, it will stay at rest.
If multiple force vectors add to a magnitude greater than zero, the object accelerates in the direction of the sum of the forces.
3) For every action, there is an equal and opposite reaction. For example, when you push your hands together, and they aren’t moving, each pushes equally into the other.
We will focus on Law #2: a body only accelerates when acted upon by an unbalanced force. So if multiple forces act on an object, we must add the force vectors to see if they are balanced or not. The results allow us to analyze how wind and ocean currents move around the globe.
Balanced Forces Web App
Click on the button “Balanced Forces web app” for an unlimited number of practice sets of 3 or 4 force vectors. An “easy” setting stresses adding vectors graphically, and a “challenging” setting focuses on calculating and adding vector components mathematically. Visual and numerical solutions are shown for each problem.
Click the button to run the web app.
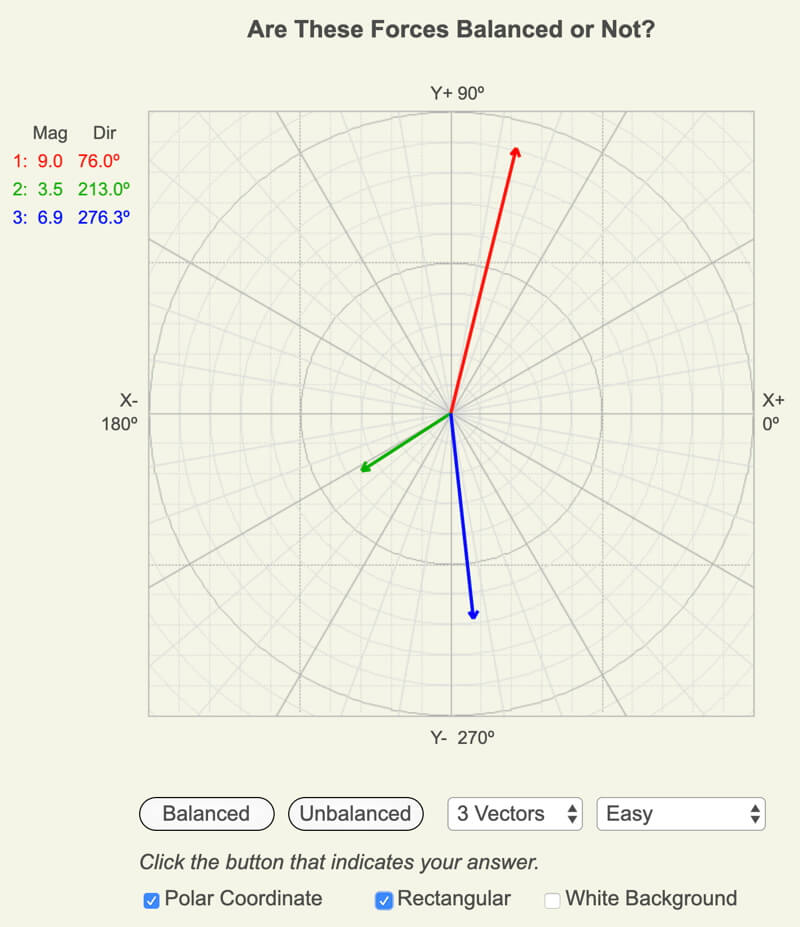
Screenshot of Balanced Forces web app. Decide if the 3 or 4 forces being displayed are balanced or not.
Benefits of Running the Web App
Although you can view the following illustrations and animations made using the Balanced Forces web app, running it on your own has several advantages:
- The images will be larger.
- You may view any image as long as you like, so you may study and/or draw those that help you most.
- There are additional visualizations and activities to explore.
- Test your understanding by predicting the outcome of new settings before making the change in the app.
- You may save screenshots of visualizations you created.
Suggestion: If you have set your computer screen/computer to sleep at a short time interval, you will lose what you are viewing when running the web app. Consider changing your settings to give yourself time to work with the app as you like.
3 Forces: Balanced or Unbalanced?
Examine the diagrams of three forces that follow to see if they are balanced or not. If unbalanced, which direction will the object accelerate?
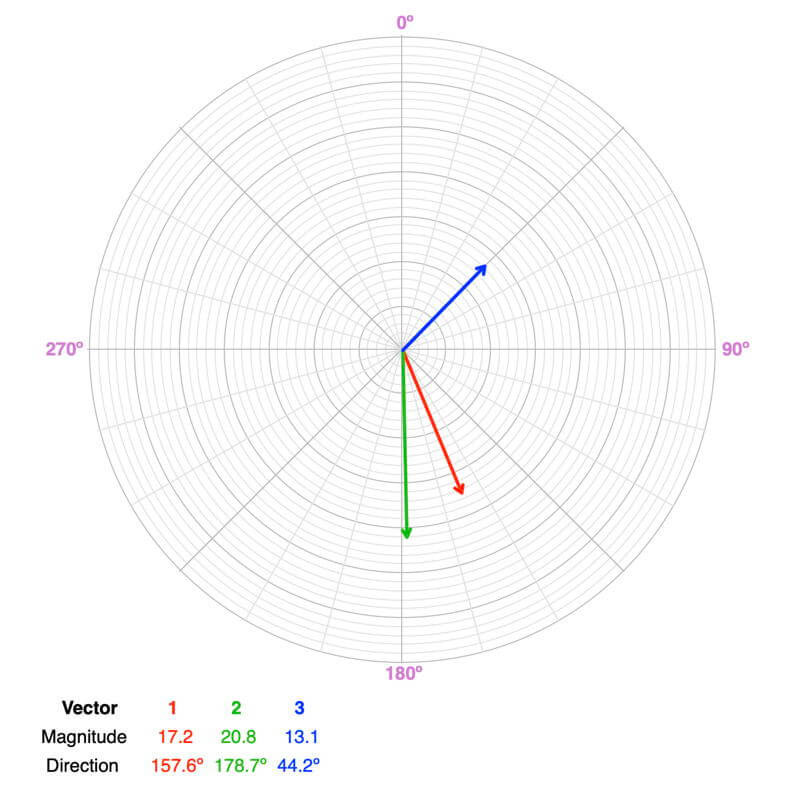
Balanced or Unbalanced?
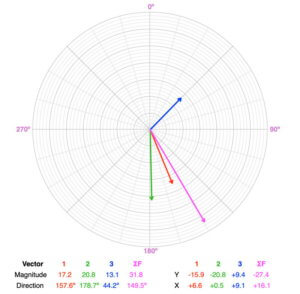
Unbalanced. None of the forces have directions between 180º and 360º (0º). There aren’t any forces to counterbalance the net southeastern pull of the three forces.
The resultant force vector (magenta) has a magnitude of 31.8 and a direction of 149.5º, so the object will accelerate in this direction. It will remain accelerating in this direction if the force vectors remain the same over time.
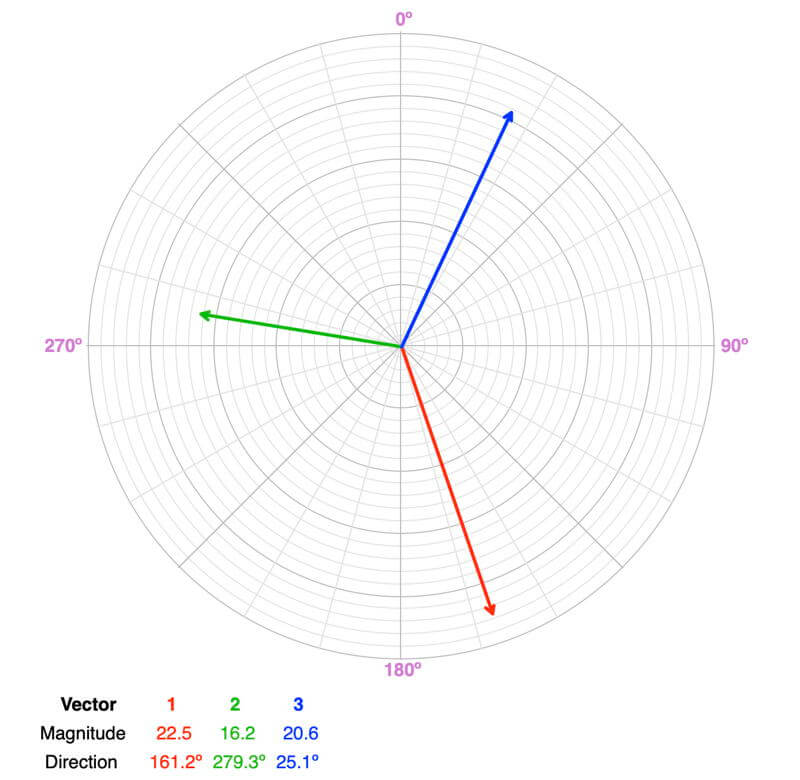
Balanced or Unbalanced?
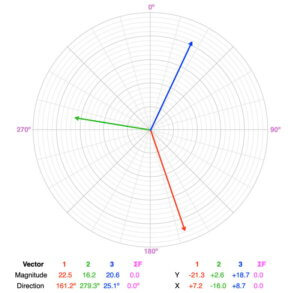
Balanced. A quick visual way to check if the forces are balanced is to add two of the vectors and see if the resultant vector is a mirror image of the third vector (same magnitude, opposite direction). Adding the blue and green vectors creates a mirror image of the red vector. Note: there are three combinations of which two vectors you add to compare to the third.
The object will not accelerate. If it is moving, it will remain moving in the same direction at the same speed. If it is at rest, it will stay that way.
Balanced or Unbalanced?
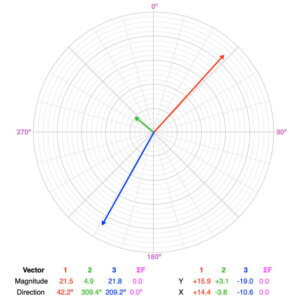
Balanced. A quick visual way to check if the forces are balanced is to add two of the vectors and see if the resultant vector is a mirror image of the third vector (same magnitude, opposite direction). Adding the blue and green vectors creates a mirror image of the red vector. Note: there are three combinations of which two vectors you add to compare to the third.
The object will not accelerate. If it is moving, it will remain moving in the same direction at the same speed. If it is at rest, it will stay that way.
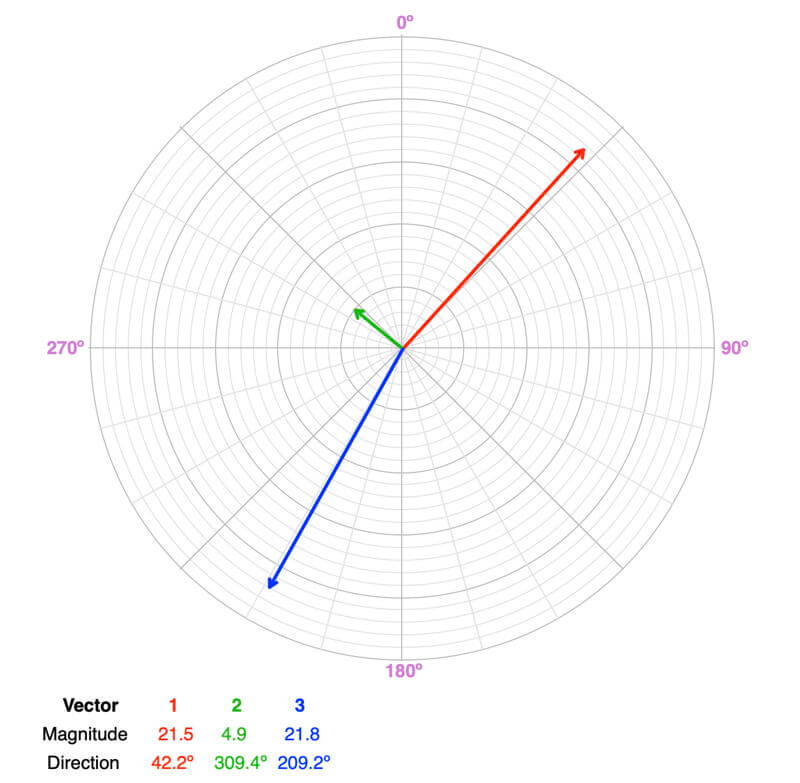
Balanced or Unbalanced?
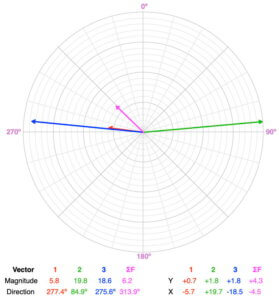
Unbalanced. None of the forces have directions less than 90º and greater than 270º. There aren’t any forces to counterbalance the net northwestern pull of the three forces.
The resultant force vector (magenta) has a magnitude of 6.2 and a direction of 313.9º, so the object will accelerate in this direction. It will remain accelerating in this direction if the force vectors remain the same over time.
4 Forces: Balanced or Unbalanced?
When we explore moving air (wind!), four forces may be involved in creating the wind’s direction and speed. So, we need to practice using four force vectors.
Examine the diagrams of four forces that follow to see if they are balanced or not. If unbalanced, which direction will the object accelerate?
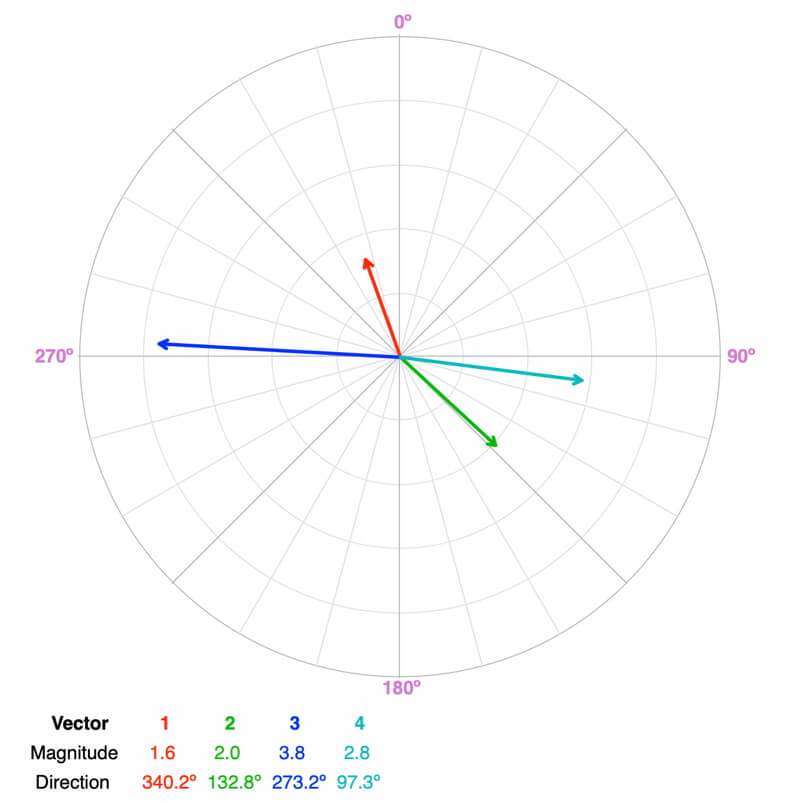
Balanced or Unbalanced?
Balanced. A quick visual way to check if the forces are balanced is to add two of the vectors and see if the resultant vector is a mirror image of the sum of the remaining two vectors (same magnitude, opposite direction). Adding the red and blue vectors creates a mirror image of the sum of the green and cyan vectors. Note: there are four combinations of which two vectors you add to compare to the sum of the remaining two.
The object will not accelerate. If it is moving, it will remain moving in the same direction at the same speed. If it is at rest, it will stay that way.
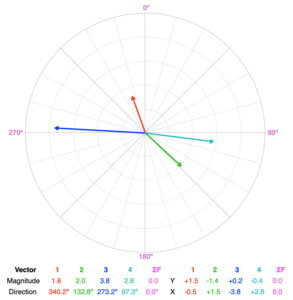
Balanced or Unbalanced?
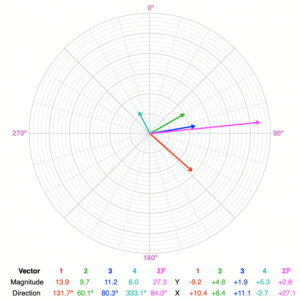
Unbalanced. None of the forces have directions between 120º and 300º. There aren’t any forces to counterbalance the net pull of the four forces toward the east.
The resultant force vector (magenta) has a magnitude of 27.3 and a direction of 84.0º, so the object will accelerate in this direction. It will remain accelerating in this direction if the force vectors remain the same over time.
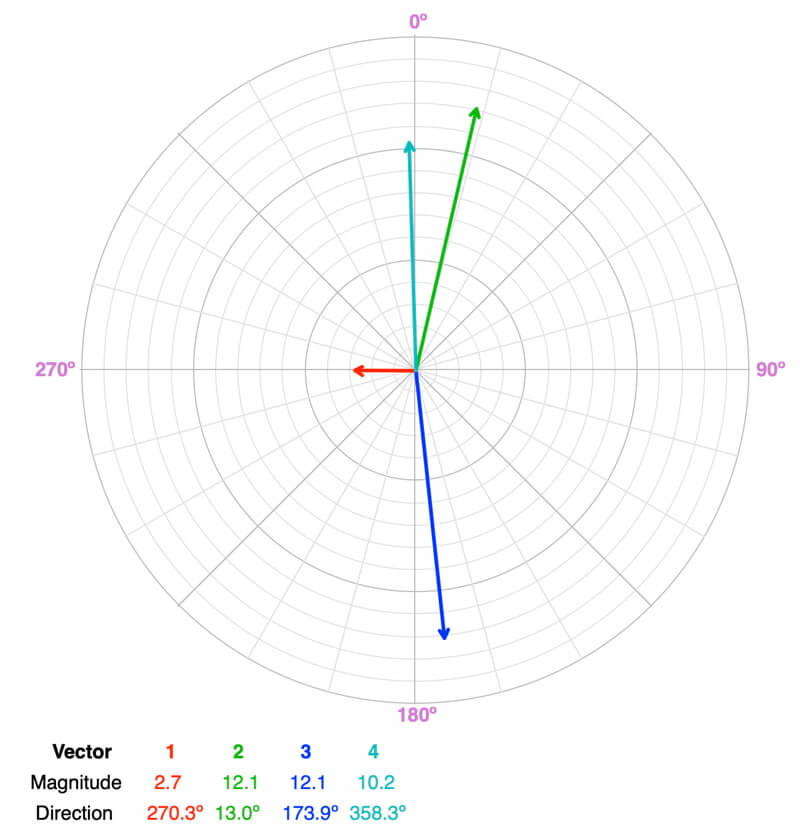
Balanced or Unbalanced?
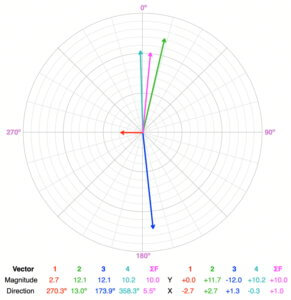
Unbalanced. Adding the green and cyan vectors creates a resultant that is in roughly the opposite direction of the sum of the red and blue vectors. However, the magnitudes of each are much different.
The resultant force vector (magenta) has a magnitude of 10.0 and a direction of 5.5º, so the object will accelerate in this direction. It will remain accelerating in this direction if the force vectors remain the same over time.
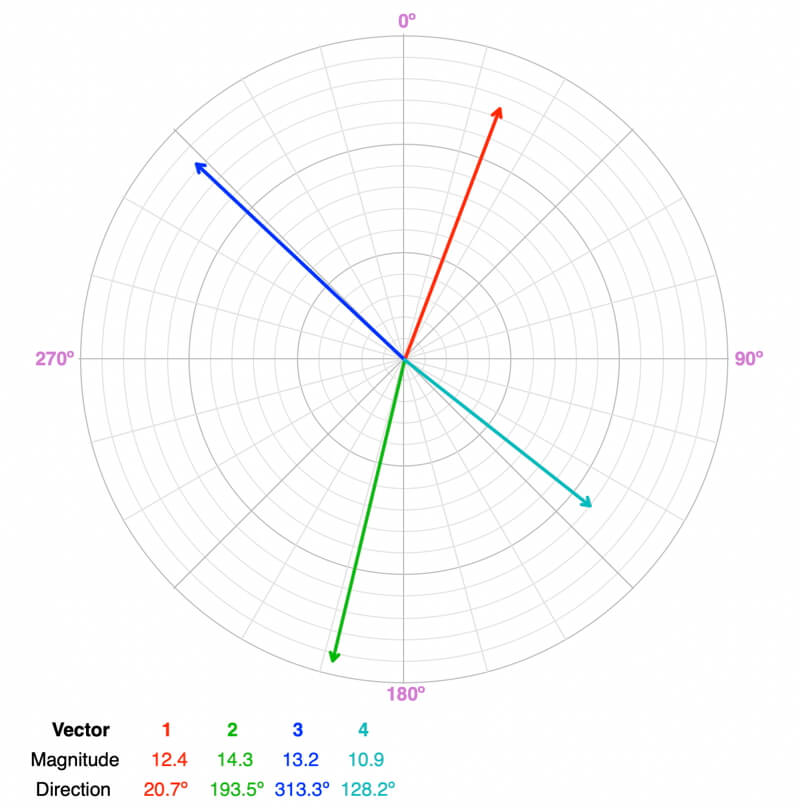
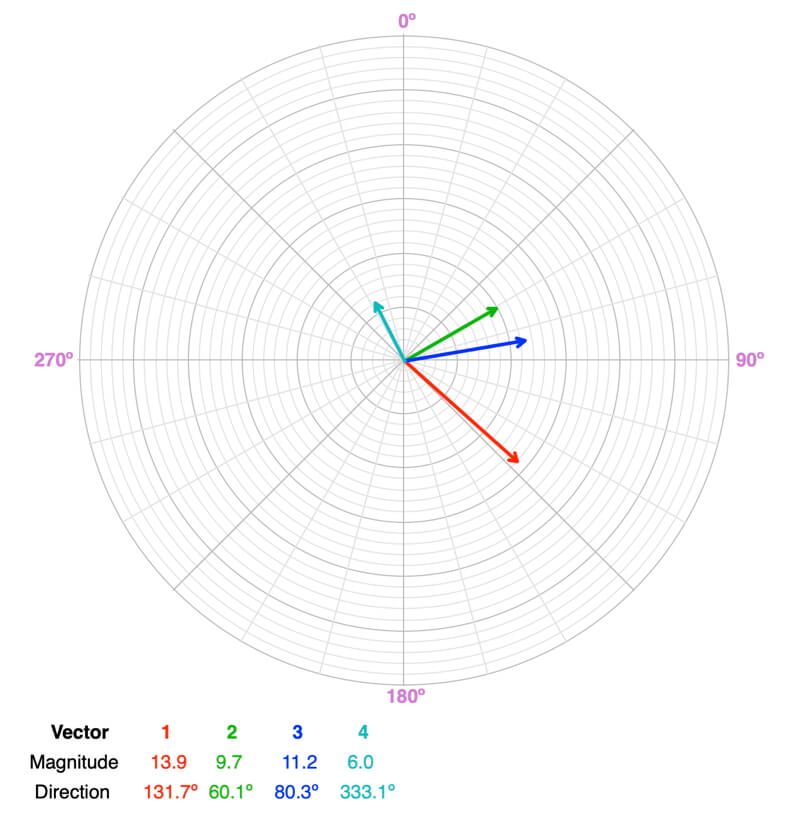
Balanced or Unbalanced?
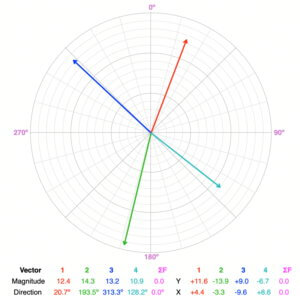
Balanced. A quick visual way to check if the forces are balanced is to add two of the vectors and see if the resultant vector is a mirror image of the sum of the remaining two vectors (same magnitude, opposite direction). Adding the red and blue vectors creates a mirror image of the sum of the green and cyan vectors. Note: there are four combinations of which two vectors you add to compare to the sum of the remaining two.
The object will not accelerate. If it is moving, it will remain moving in the same direction at the same speed. If it is at rest, it will stay that way.
Changing Forces
In most introductory physics courses, forces are often constant. For many of Earth processes, including the wind, forces change over distance and time. These are challenging problems to calculate, and that isn’t the intent of these activities. Instead, conceptually understanding and applying vectors and forces helps us explore the general flow patterns within our atmosphere, oceans, and even inside the Earth.

I enjoy reading through an article that can make people think.
Also, thanks for permitting me to comment!