Vectors And Forces
Earth’s Moving Fluids
Wind and ocean currents carry heat and essential matter around the planet, making most of it habitable. But how fast and where do they move? We need to use vectors since they contain information on magnitude and direction.
Note: You don’t need to be a math wizard to use vectors. Working through the concepts graphically allows you to make useful estimates of the behavior of winds and ocean currents around the planet. If you want more precision with your analyses, explore the math of vectors presented here.
Tall grass bent by strong winds on a sunny day.
Vectors
A vector is a quantity that has both magnitude and direction. When drawn, it is typically represented by an arrow whose direction is based on the accepted axes and whose length is proportional to the quantity’s magnitude. Examples of vectors in Earth Systems: temperature gradient, displacement, velocity, acceleration, force, wind, and ocean current. Quantities with only a magnitude are scalars, such as distance, temperature, energy, and mass.
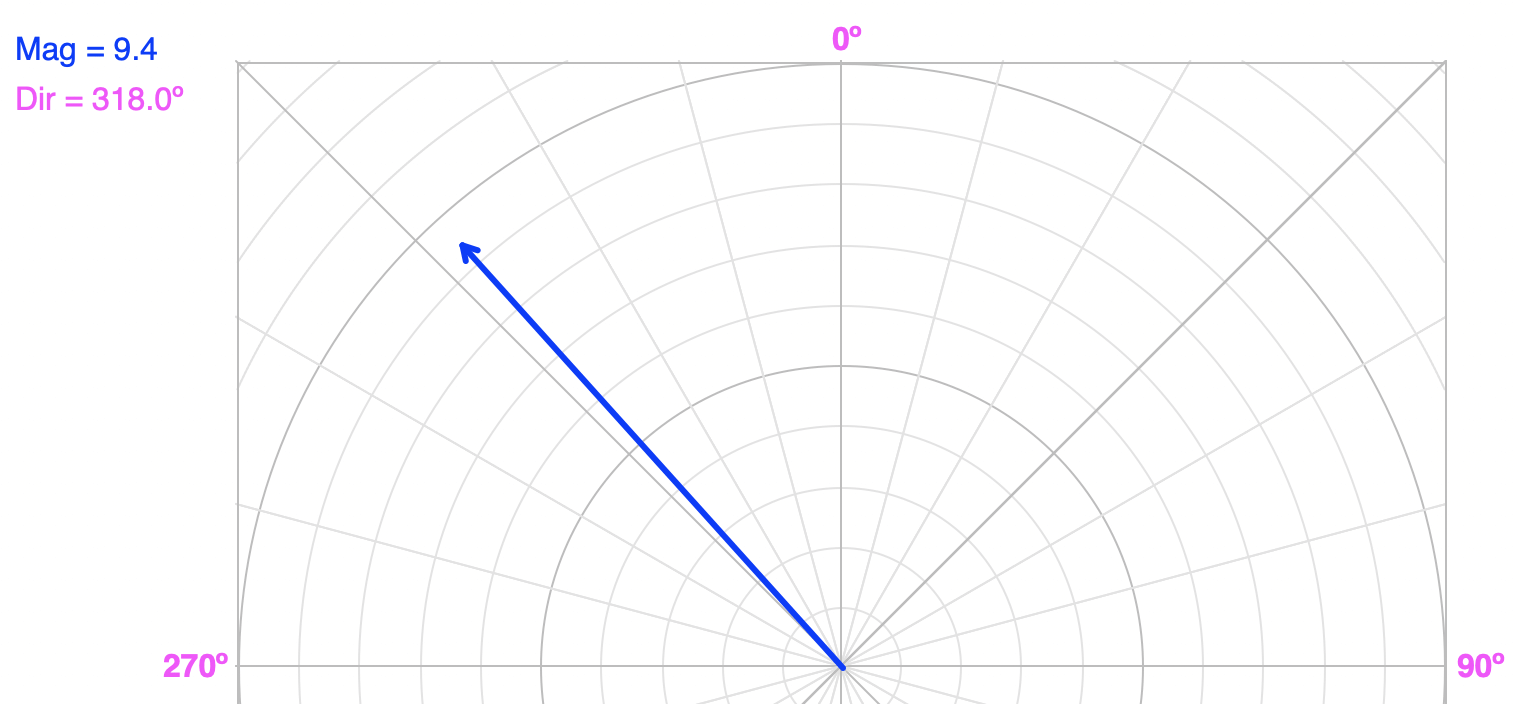
An example of a vector drawn as an arrow. The length of the arrow is proportional to the vector’s magnitude. The arrow points in the vector’s direction based on the navigation convention in this case.
The beauty of vectors is that we can change the orientation of the axes to make it easier to work with the math. This is very useful for studying many phenomena in our physical world. We often use ‘x’ and ‘y’ when working with two dimensions. If working in three dimensions, the third axis is usually ‘z’. Key for 2 or 3D: the axes must be perpendicular to each other. This allows for information to be separate from each axis. If you took one step exactly north, your east/west position would not change.
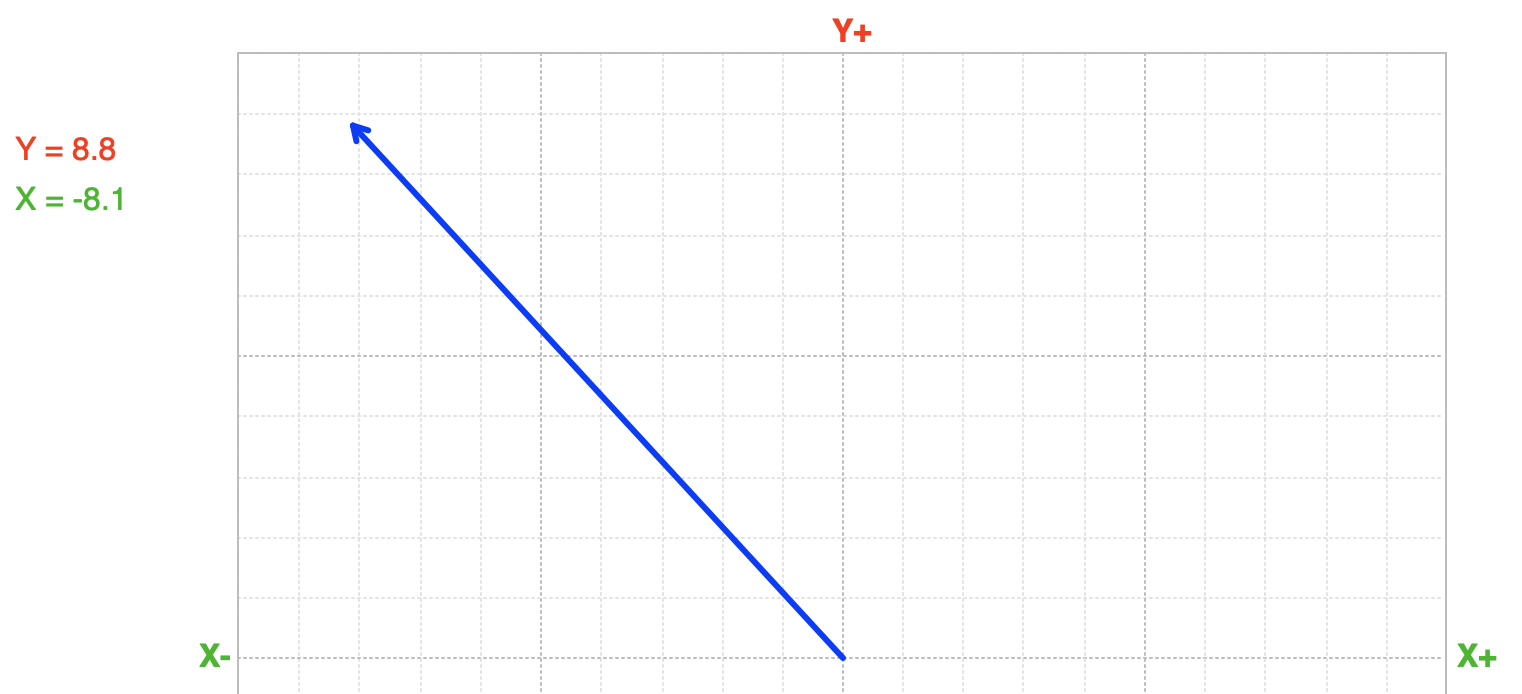
Vectors are defined by any set of perpendicular axes, even if the axes are oriented in whatever direction best suits the scenario.
Magnitude and Direction or Axial Components?
When working with vectors, which should you use? It turns out that both have strengths and drawbacks, so you should become familiar with both. Vector direction and magnitude are quite useful in working with navigation since that is how you will actually be traveling. We tend to like going in a straight line rather than a stair-step pattern of east/west and north/south patterns. Vector components allow us to work with vectors mathematically, and the results are often converted back to magnitude and direction.
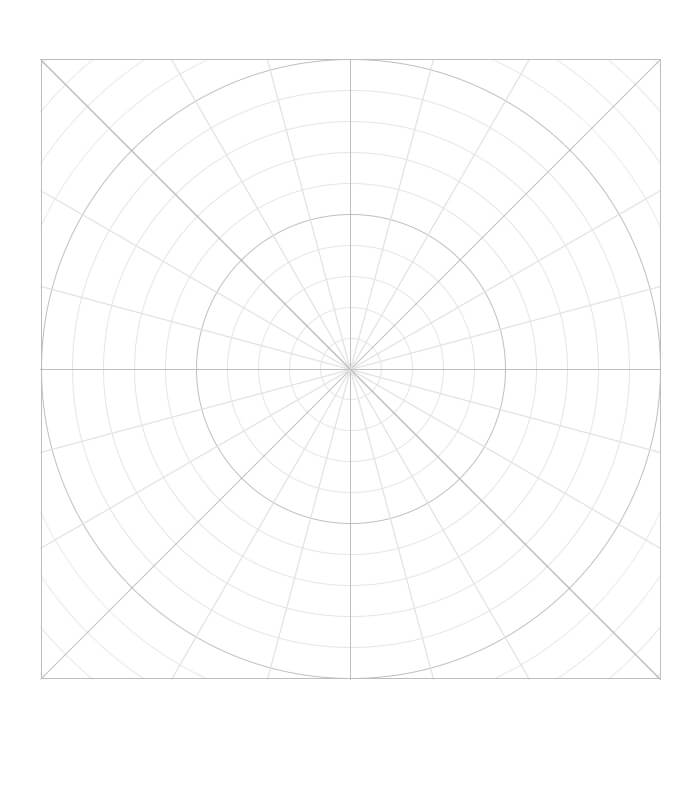
A polar coordinate grid is useful to plot vectors when given their magnitude and direction. Click on the image to download a .pdf to print.
A rectangular coordinate grid is useful to plot vectors when given their axial components. Click on the image to download a .pdf to print.
Combined polar and rectangular coordinate grids are useful for plotting and converting vectors between magnitude and direction and axial components. Click on the image to download a .pdf to print.
Convention of Vector Directions
For navigation, moving at a bearing of 0º means you are traveling northward, and the angle increases clockwise. A bearing of 90º means traveling toward the east. In meteorology, wind vectors use a different convention. A 0º wind blows from the north, not going toward the north. Wind direction increases clockwise, as navigation does. In trigonometry 0º points along the positive x-axis and direction increases counterclockwise. These dramatic differences illustrate that it is very important to know the conventions of direction for the vectors you are working with.
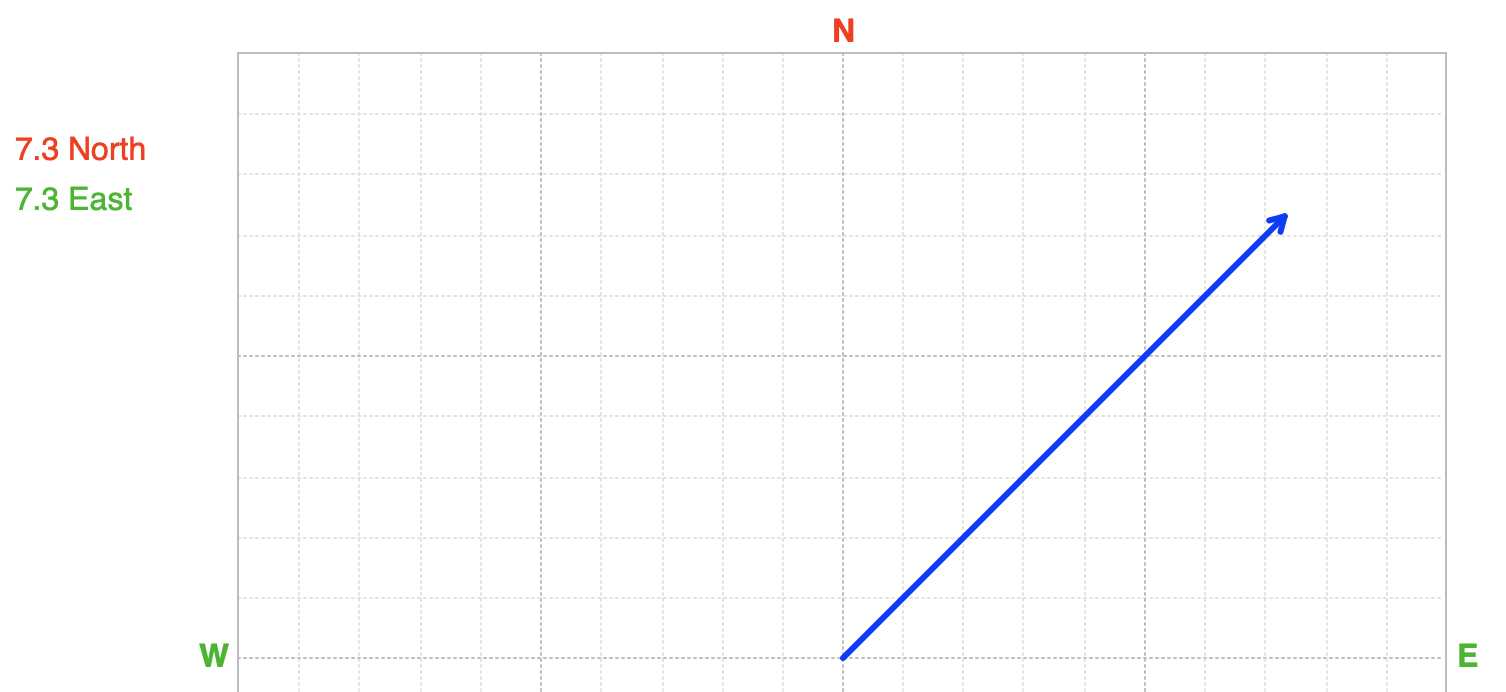
An example of a vector where the magnitudes of the vector’s directional components shown.
How Vectors Change with Magnitude
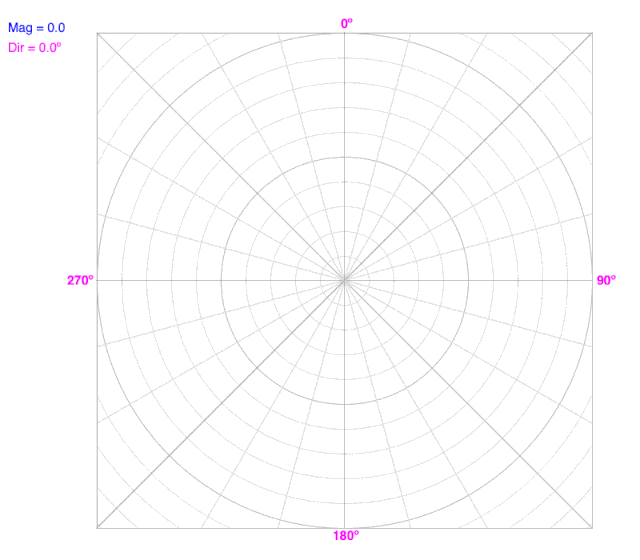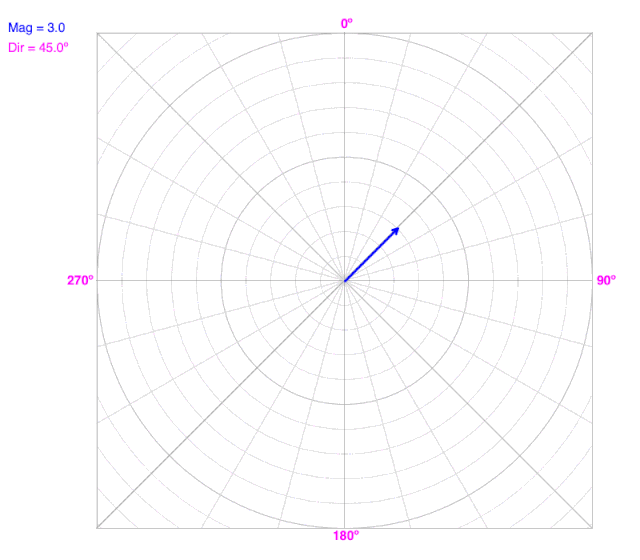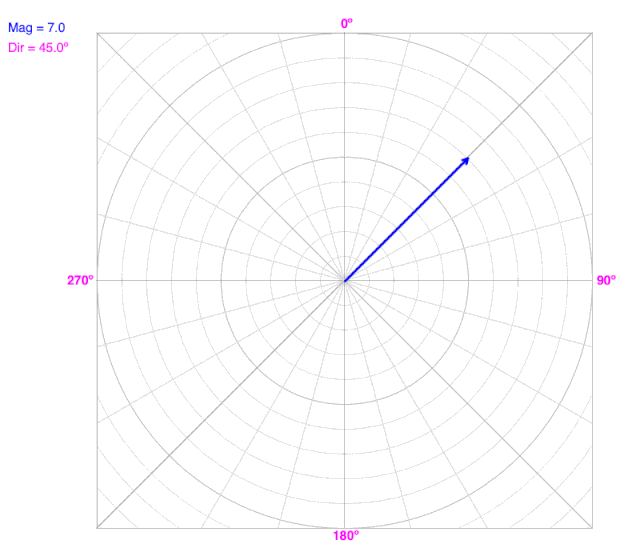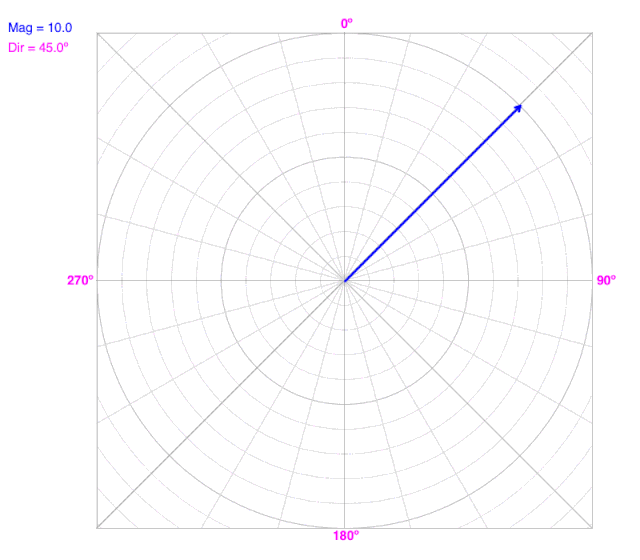
What do you observe?
Magnitude cannot be negative. As magnitude increases, the vector moves radially away from the origin in the vector’s direction.
Notice that both the X- and Y-components change as magnitude changes, but the direction doesn’t change.
How Vectors Change with Direction
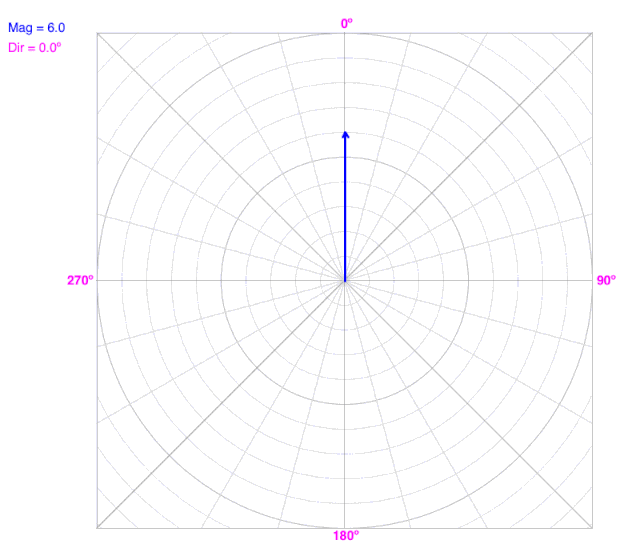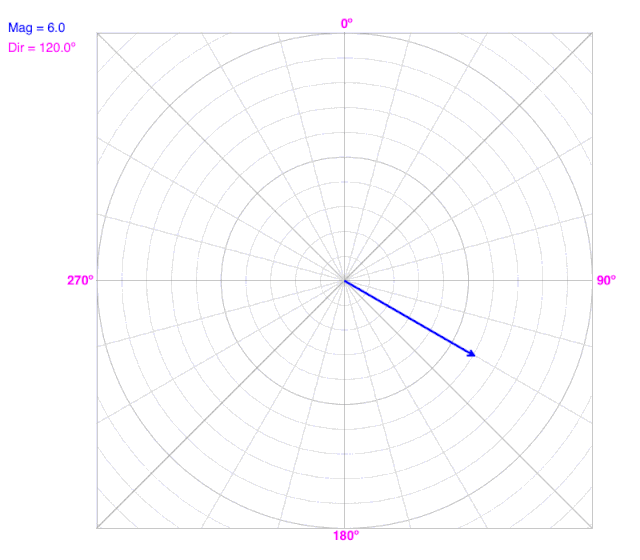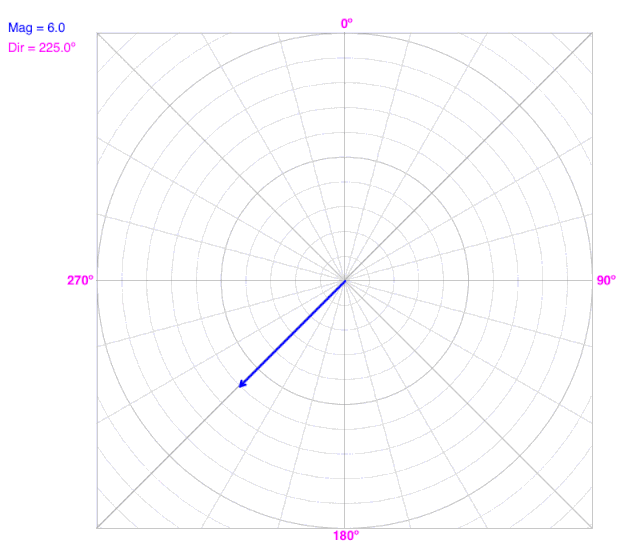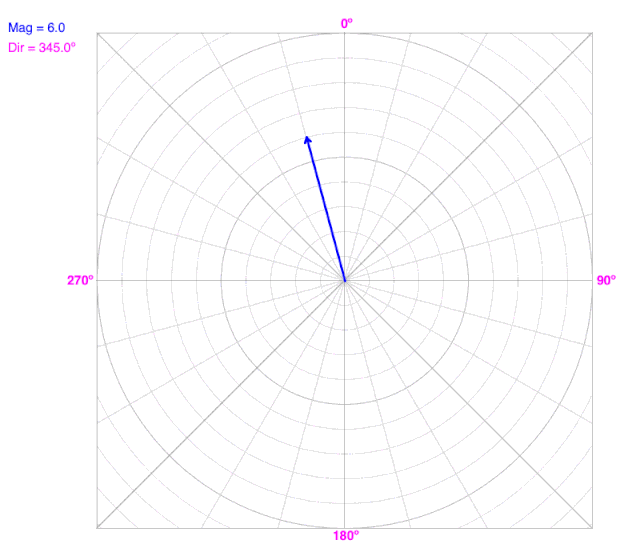
What do you observe?
This is the navigation convention for direction. The positive Y-axis or North is 0º, and direction increases clockwise.
Notice that the X- and Y-components change as direction changes, but the magnitude doesn’t change.
How Vectors Change with the X-component
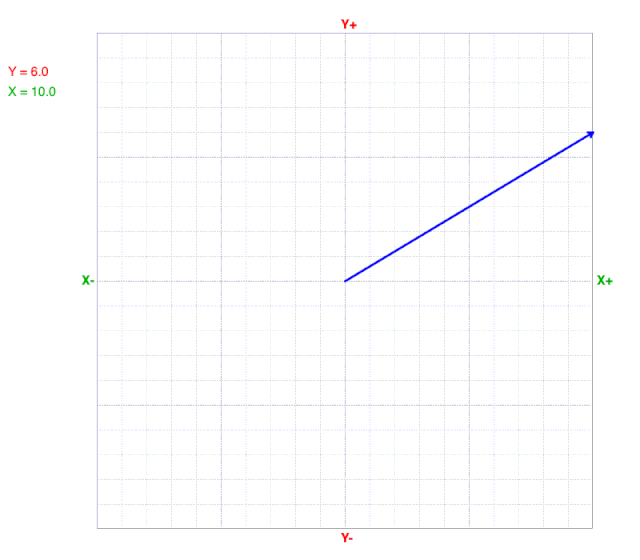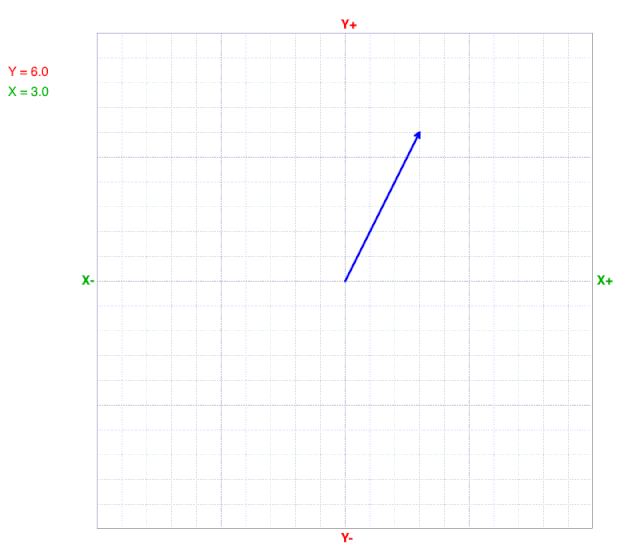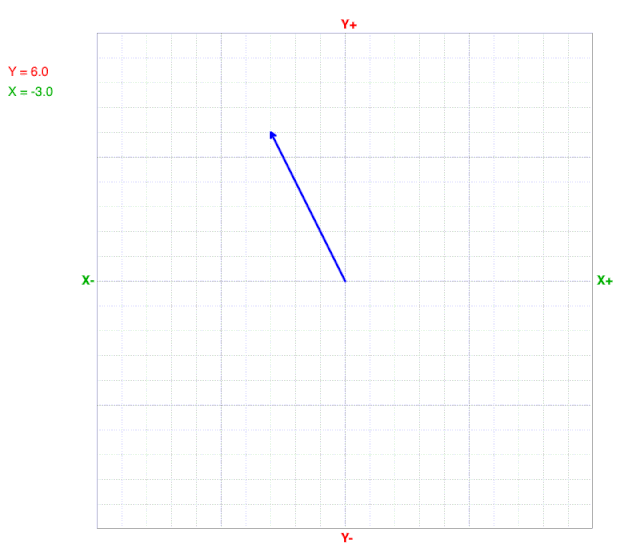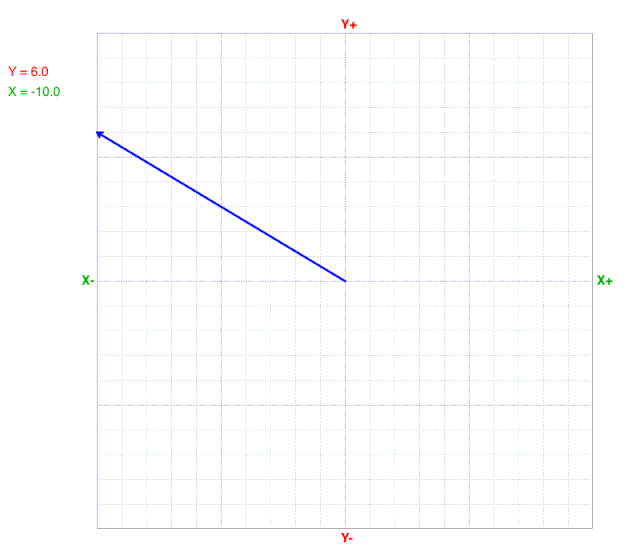
What do you observe?
As the X-component decreases, the tip of the vector moves from right to left.
Notice that both the magnitude and direction change as the X-component changes, but the Y-component doesn’t change.
How Vectors Change with Y-component
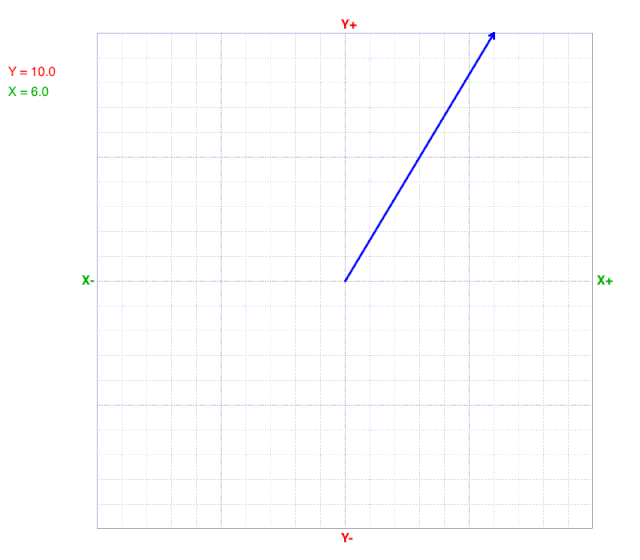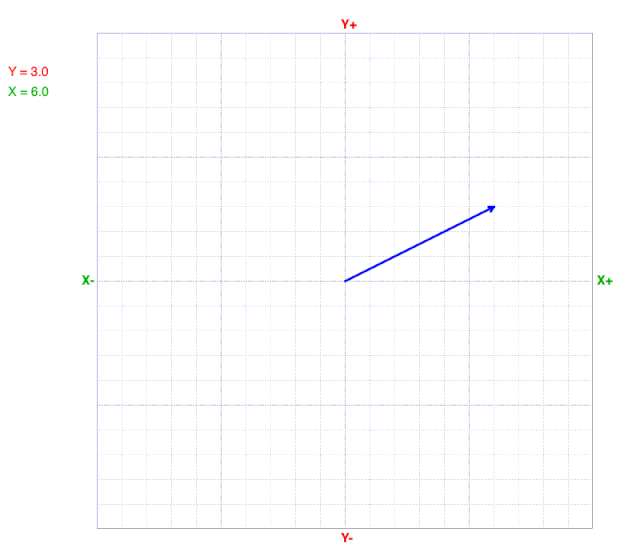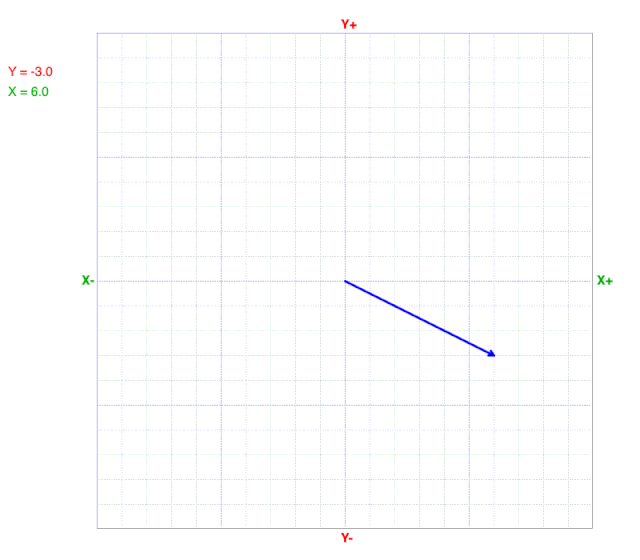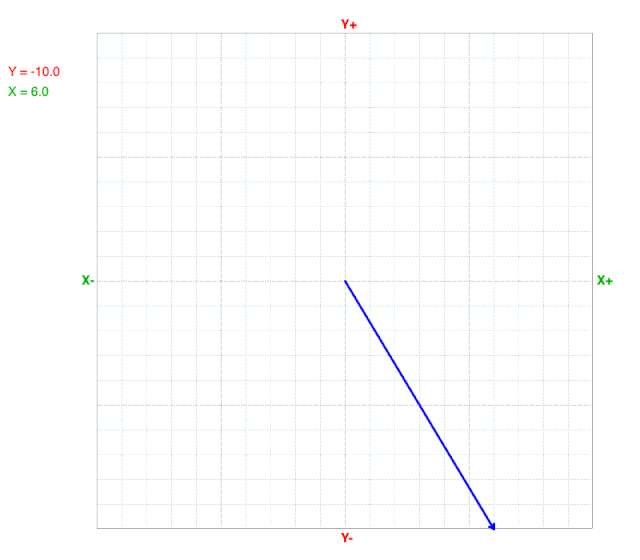
What do you observe?
As the Y-component decreases, the tip of the vector moves from top to bottom.
Notice that both the magnitude and direction change as the Y-component changes, but the X-component doesn’t change.
Navigate the Color World with Vectors
Practice navigating with vectors as you explore two worlds of color.
Study the world of additive color, which is how our eyes see and how cameras detect color. The world of subtractive color is how dyes, pigments, and paints create color.
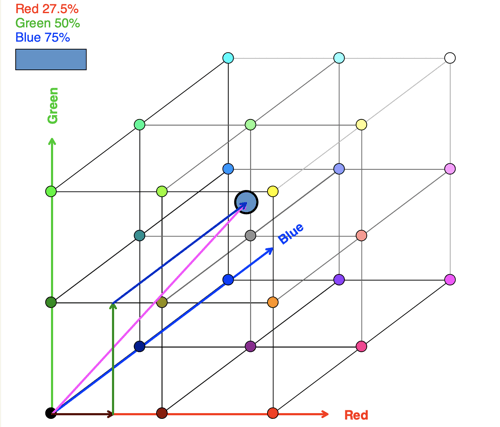
An example of a color identified within the Red, Green, Blue colorspace.
0 Comments