← Color Vectors | Adding Vectors →
Right Triangles and Vectors
A right triangle has one angle equal to 90º, or a right angle. The hypotenuse is the side opposite the ‘right’ angle, and it will always be the longest side of a right triangle.
The two remaining angles inside the triangle are less than 90º, and adding the two together always equals 90º.
If we label one of the angles less than 90º as θ, the sides of the triangle may be labeled relative to θ. There is the side opposite θ, and the side that extends from θ called the adjacent side.
Right Triangles and the Pythagorean Theorem
The Pythagorean Theorem applies to right triangles: the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two shorter sides.
Opposite2 + Adjacent2 = Hypotenuse2
NOTE: to save space and also make the text less cumbersome to read (and write), we will use the following conventions:
-
- opposite = length of the side opposite the designated angle of the right triangle
- adjacent = length of the side adjacent to the designated angle of the right triangle
- hypotenuse = length of the longest side of the right triangle
If you are familiar with vectors, click the button to run the web app to practice manipulating vectors. Considerable support materials about vectors follow, as well as another button to run the app.
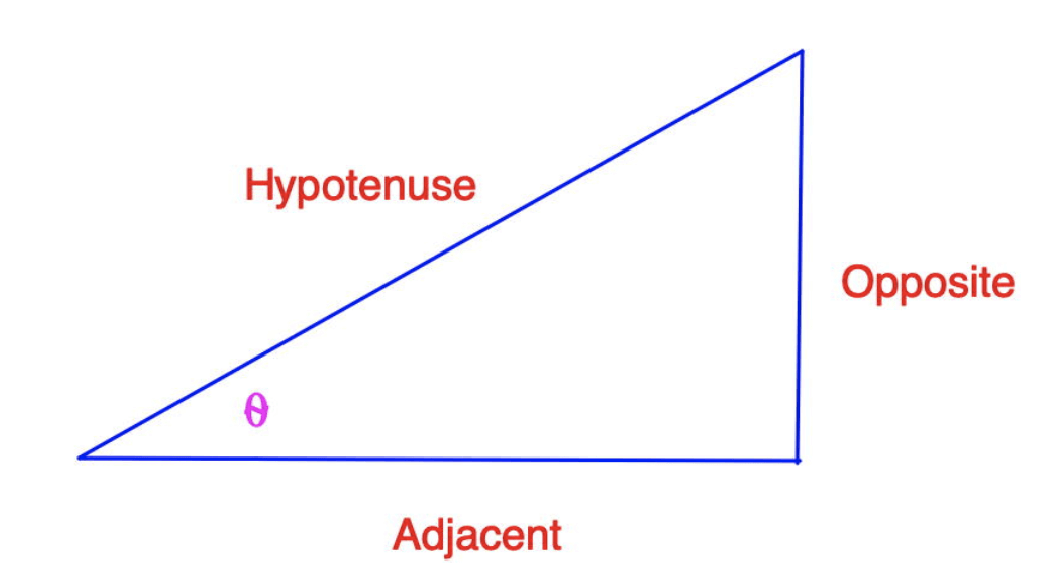
A right triangle has two acute angles (angles less than 90º). In the diagram above, the angle theta (θ) has one side opposite it, and another adjacent to it.
Right Triangles and Trig Functions
When analyzing variables associated with right triangles, the ratio, H/L, keeps popping up again and again. For instance, consider the large right triangle with hypotenuse 2L and vertical side length 2H. Insert a similar right triangle a vertical side length of H. This means that its hypotenuse is only L. Both triangles have the same angle of inclination, θ. Both H/L and θ indicate the pitch or slope of the ramp.
When a quantity keeps appearing in a calculation’s final form, mathematicians, scientists, and engineers pay attention. They gave the quantity its own name. H/L is called “sine of θ.”
sine(θ) = sin(θ) = H / L = opposite / hypotenuse
The base of the triangle, W, is also significant in other physical phenomena. W is the side adjacent to θ. The ratio W/L is the cosine of θ:
cosine(θ) = cos(θ) = W / L = adjacent / hypotenuse
In addition, there is a function that involves both the sin and cos functions. The tangent of θ is defined as:
tangent(θ) = tan(θ) = H / W = opposite / adjacent = sin(θ) / cos(θ)
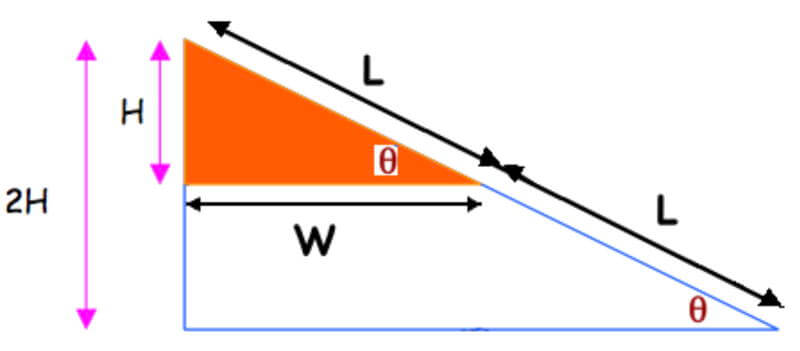
H / L = 2H / 2L = something to do with angle θ.
Trigonometry functions are simply the ratios of sides of a right triangle relating to one of the acute angles in the triangle.
Magnitude and Direction ⇔ Axial Components
When working with vectors, which should you use? It turns out that both have strengths and drawbacks, so you should become familiar with both. Vector direction and magnitude are quite useful in working with navigation since that is how you will actually be traveling. We tend to like going in a straight line rather than a stair-step pattern of east/west and north/south patterns. Vector components allow us to work with vectors mathematically, and the results are often converted back to magnitude and direction.
Use the examples that follow to convert between these two forms of vectors.
Calculating Vector Components from Magnitude & Direction
Since the axes that define the direction of a vector are perpendicular to each other, a right triangle also describes a vector relative to the axes. This spatial relationship means that we use trig functions to find the axial components of vectors if we know the magnitude and direction. First, identify the angle to an axis of interest and then apply the appropriate trig function. In all cases, the hypotenuse will be the magnitude of the vector.
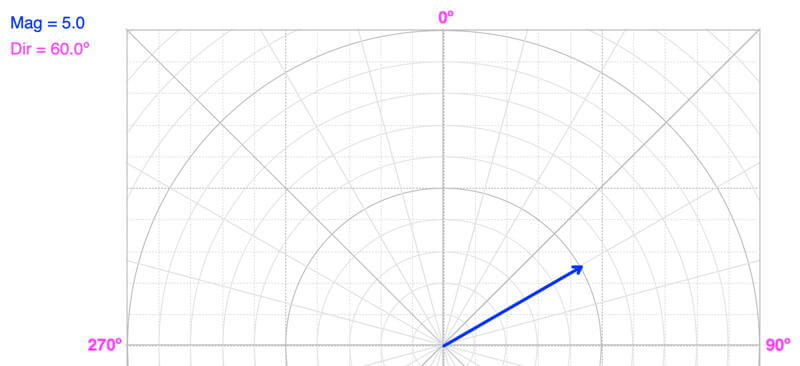
To convert magnitude and direction to the axial components, use trig equations. The vector drawn on the right is 60º clockwise from the y-axis (which is north when using the convention for navigation). This means the side opposite 60º is parallel to the x-axis (East/West), and the adjacent side is parallel to the y-axis (North/South).
To find the component in the East/West direction (or X):
Opposite = X component = Magnitude * sin(Direction) = 5.0 * sin(60º) = 4.3 East
and to calculate the North/South (or Y) component:
Adjacent = Y component = Magnitude * cos(Direction) = 5.0 * cos(60º) = 2.5 North
The vector above is drawn using the navigation convention for direction, where 0º is pointing north and angles increase clockwise. In trigonometry, the convection is that 0º points along the positive x-axis, and angles increase counterclockwise.
Click on the image to download a .pdf of the polar coordinate grid.
Inverse Trig Functions
At every step in learning mathematical operations, we learn how to “undo” it at the same time. Addition and subtraction were taught together since each “undoes” the other. Now we need to learn how to undo the trig functions so we can calculate the angle if we know the ratio of the sides of a right triangle.
For the trig functions, the inverse functions are identified with a “-1” superscript or an “a” precedes the function.
Inverse sin(θ) = asin(θ) = sin¯¹(θ)
This means that asin(sin(θ)) = θ and asin(Opposite / Hypotenuse) = θ.
Similarly,
acos(Adjacent / Hypotenuse) = θ
and
atan(Opposite / Adjacent) = θ.
On your calculator, this is sin¯¹, inv sin, arcsin, or asin. The inverse cosine is cos¯¹, inv cos, arccos, or acos, and inverse tangent is tan¯¹, inv tan, arctan, or atan.
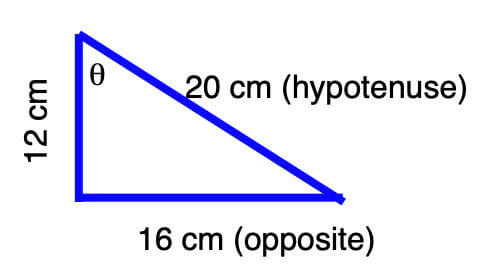
For example, calculate θ for a right triangle where the hypotenuse is 20, the side opposite θ is 16, and the adjacent side is 12 (see the diagram above).
θ = asin(16/20) = asin(0.8) = 53.13°
We can also use the hypotenuse and the adjacent side:
θ = acos(12/20) = acos(0.6) = 53.13°
And last but not least, we can use the opposite and adjacent sides:
θ = atan(16/12) = atan(1.333) = 53.13°
Calculating Magnitude & Direction from Vector Components
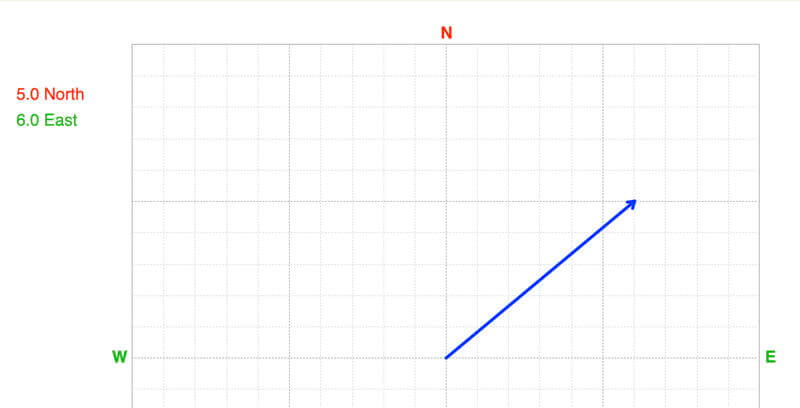
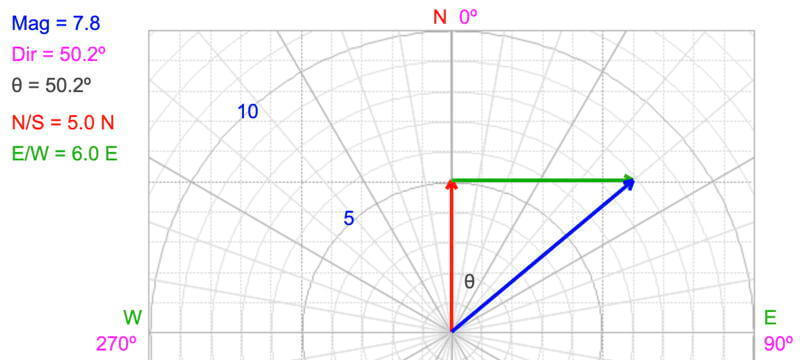
If we know the vector components, we use the Pythagorean Theorem to calculate the vector’s magnitude.
Magnitude = √(5.0² + 6.0²) = 7.8
Use the inverse trig functions to calculate the vector’s direction. When using the navigation convention (0º is north or in the positive y-direction) and direction increases clockwise), the vector’s direction is 50.2º:
Direction = tan¯¹(opposite / adjacent) = tan¯¹(6.0 / 5.0) = 50.2º
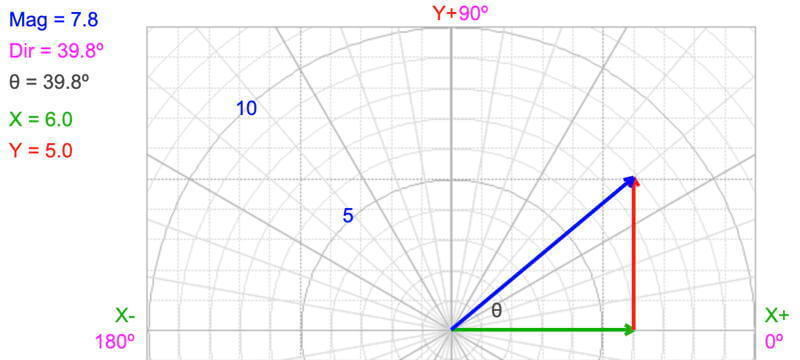
Using the trigonmetry convention (0º is in the positive x direction or East in the diagram) and direction increases counterclockwise), the vector’s direction is 39.8º:
Direction = tan¯¹(opposite / adjacent) = tan¯¹(5.0 / 6.0) = 39.8º
Click on either image above to download a blank combined polar and rectangular grids to plot and convert between magnitude and directions and axial components.
Interactively Explore Vectors
Use the Vectors web app to visualize, conceptualize, estimate, and calculate vectors in either navigation and trigonometry direction conventions. Many of the examples above came from the Vectors web app.
The Vectors web app is a combined simulation and practice app. A simulation since the vector responds to a changed variable. And a practice app since there are unlimited problems that provide visual, written, numerical, and mathematical feedback based on your answers.
Click the button to run the web app.
Common Challenges Working with Vectors
- There are several conventions on how to orient and change direction, so details are important.
- Spatial reasoning is a critical skill working with vectors, and it may be a new experience.
- Trig functions may be new as well.
- Estimations and calculations require working with values and equations in a unique sequence for a particular problem. This requires finding the right mathematical tool and interpretation when needed to solve a given step in the problem.
Acknowledgments
I would like to thank Max Hall, Amy Kumpel, and George Larivee for their many important suggestions and recommendations during beta testing.
Activities in Vectors Web App
The View activities (view vector, components, or both) focus on how magnitude and direction; the axial/directional components; and right triangles define vectors, as well as how each is spatially connected to the other.
To create a new vector, click on the graph, or select a variable to loop. Whichever variable is selected, it loops through the range of possible values, updating the display automatically to highlight the conceptual nature of vectors.
Any image displayed while using the View activities may be saved for practice, review, or test problems.
The Estimate activities provide practice estimating where the vector is located without the focus on high precision. This skill is invaluable for physics, since making quality sketches is such a critical step in solving any type of motion problem, and trigonometry too. It is also a critical skill in catching the “garbage in, garbage out” calculator moments when working with trig functions and the Pythagorean Theorem.
The Calculate activities pull all of the concepts and skills together to calculate the mag/dir or components to one-tenth of a unit. The rules for significant figures, or sig figs, are not strictly followed, but the correctness of the answer is within 0.09 of the value or less.
Benefits of Running the Web App
Although you can view these illustrations and animations made using the Vectors web app, running it on your own has several advantages:
- The images will be larger.
- You may view any image as long as you like, so you may study and/or draw those that help you most.
- There are additional visualizations and activities to explore.
- Test your understanding by predicting the outcome of new settings before making the change in the app.
- You may save screenshots of visualizations you created.
Suggestion: If you have set your computer screen/computer to sleep at a short time interval, you will lose what you are viewing when running the web app. Consider changing your settings to give yourself time to work with the app as you like.
← Color Vectors | Adding Vectors →

0 Comments