Explore Spirals
Spirals are found in nature and used in various technologies, such as springs, screws, spiral staircases (also, these are visually spectacular), paper towel rolls, and drill bits. When graphing, they are easier to create using polar coordinates compared to cartesian coordinates. In cartesian coordinates, the x and y are perpendicular to each other. Similarly, the axes of polar coordinates, radius and angle, are perpendicular. Using the following four animations, review how a change in one axis does not involve a change in the other.
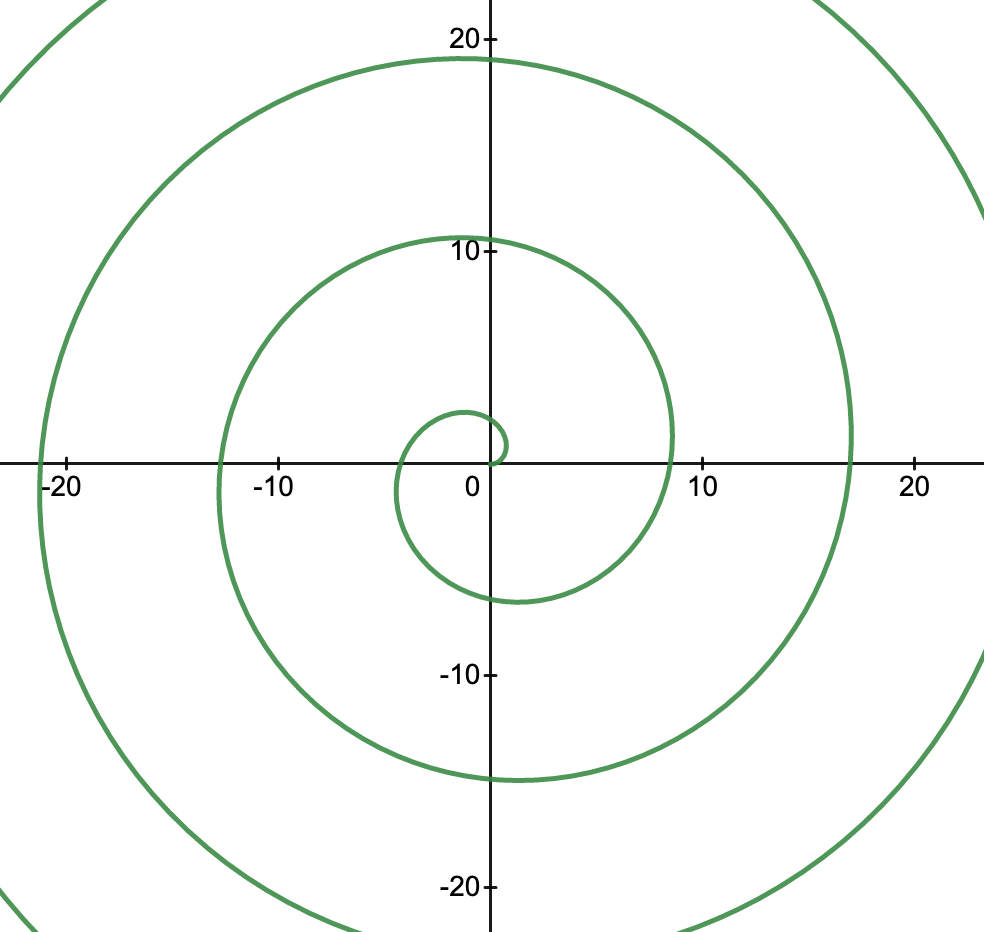
An Archimedes spiral in the graph on the right (below) was created from the equation
r = c θ
where r = radius, θ = the angle in radians from the right-most horizontal line in a counterclockwise direction, and c is a constant.
Say c = 1, then
| θ | r |
| 0 | 0 |
| π/2 | π/2 = 1.57 |
| π | π = 3.14 |
| 3π/2 | 4.71 |
| 2π | 6.28 |
| 5π/2 | 7.85 |
Open the spiral model by clicking on the graph or click here.
Some ideas for exploring the eight different types of spirals:
1) Study the distance between successive spirals and relate this to how we find spirals in nature and how we use these in art and technology.
2) Compare two spirals at a time by overlaying them.
3) Click the “play” button on the sliders to see continuous change and see what patterns you observe.
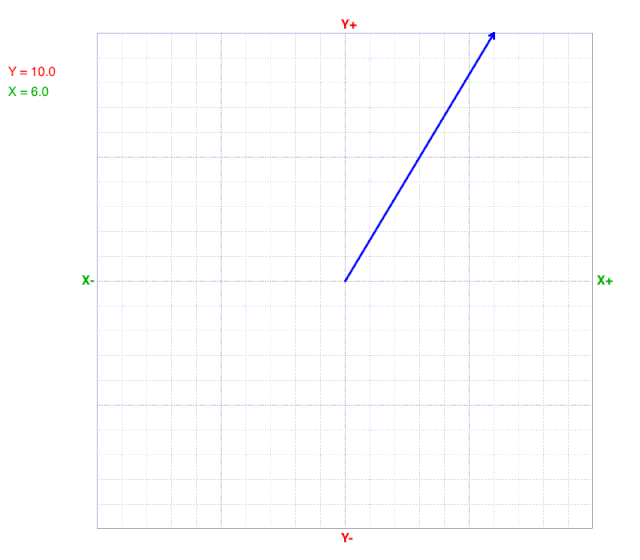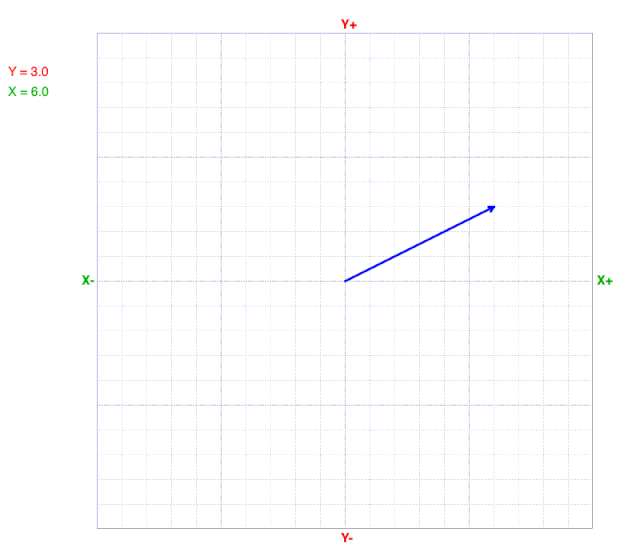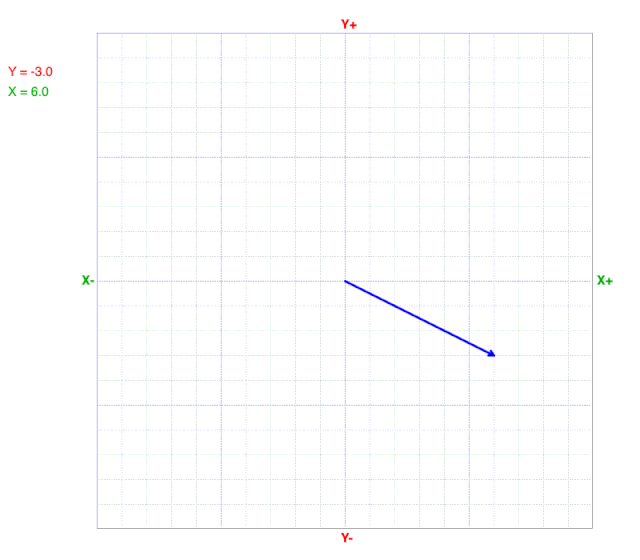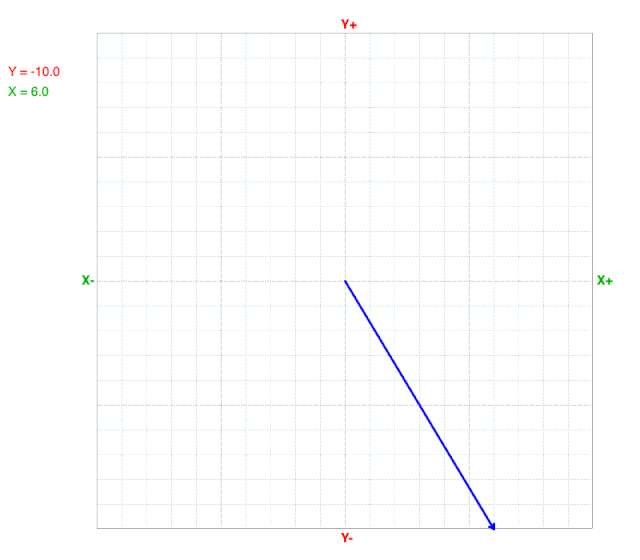
As y values change, the x value at the line’s end (arrow) does not change on a cartesian coordinate graph.
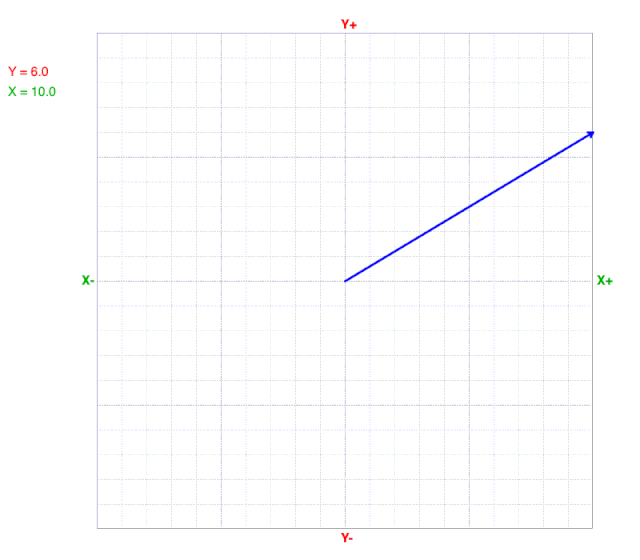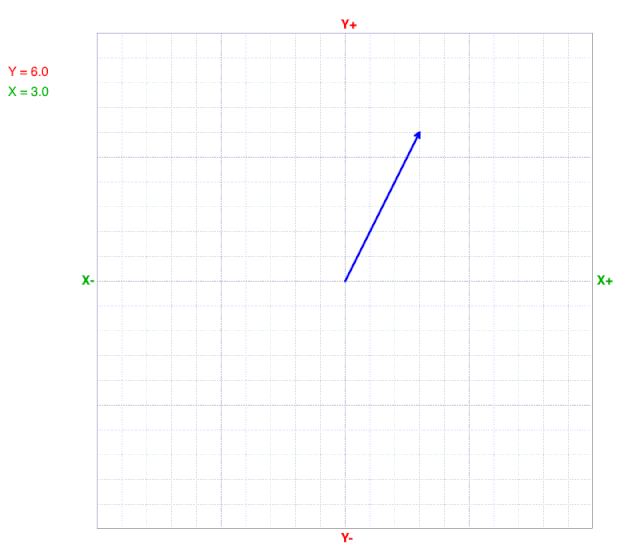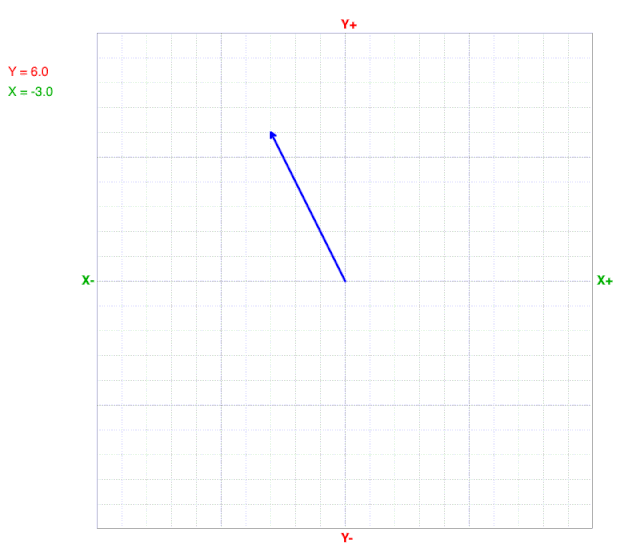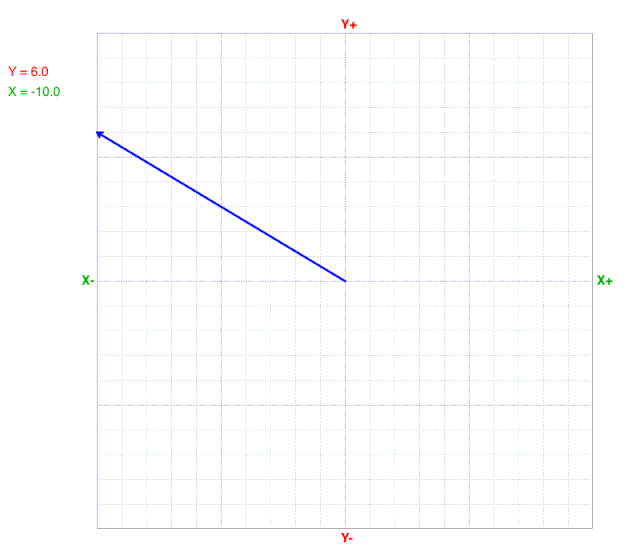
As x values change, the y value at the line’s end (arrow) does not change on a cartesian coordinate graph.
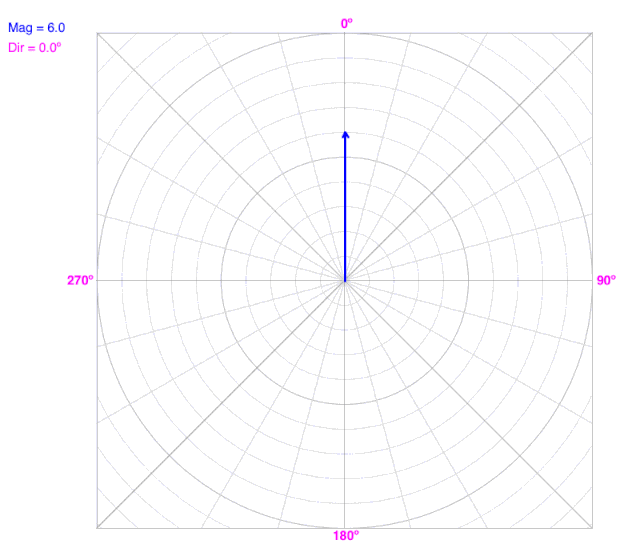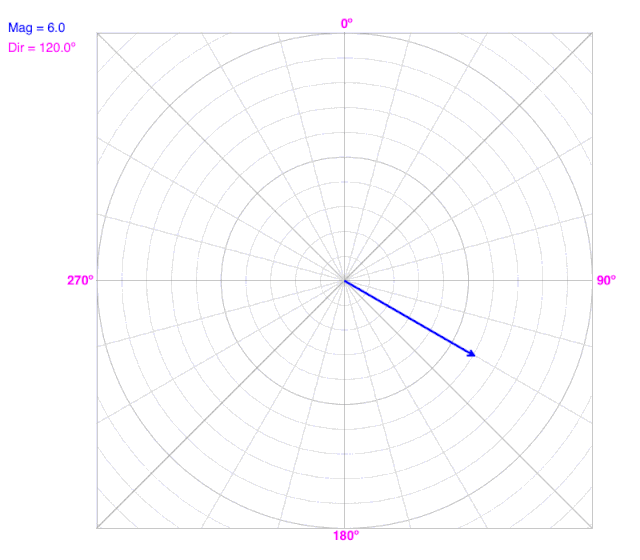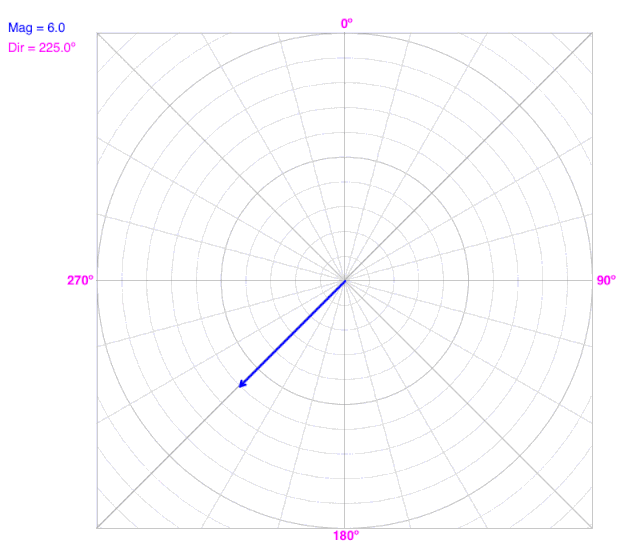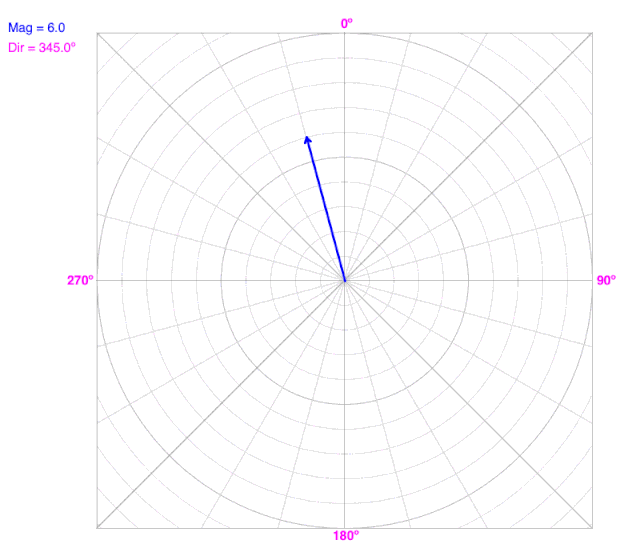
As the angle (direction) changes, the line does not change the radius on a polar coordinate graph.
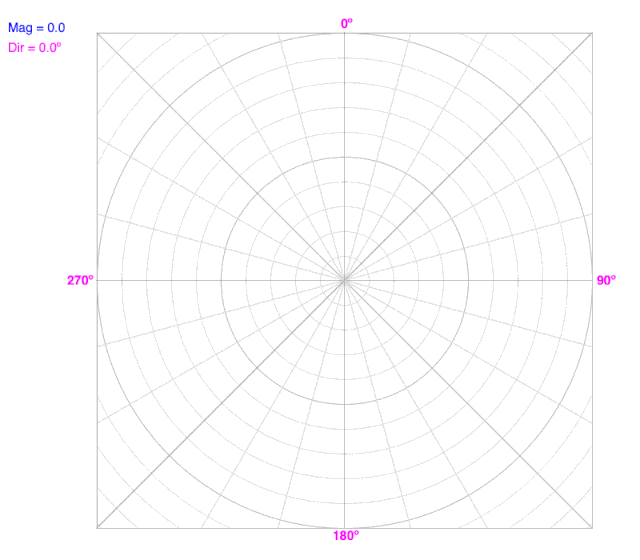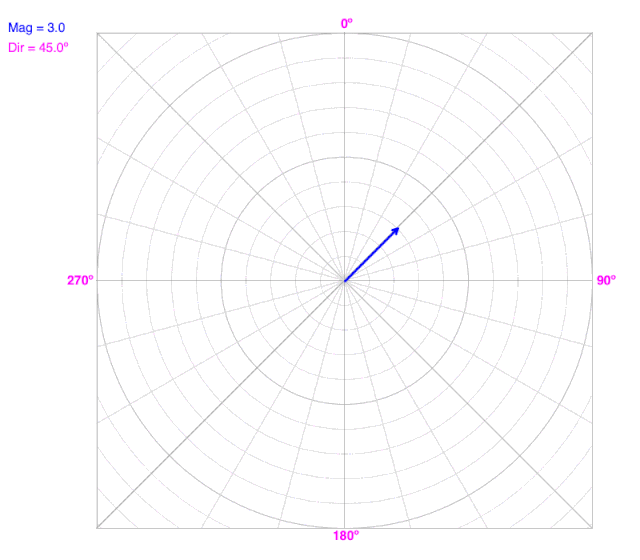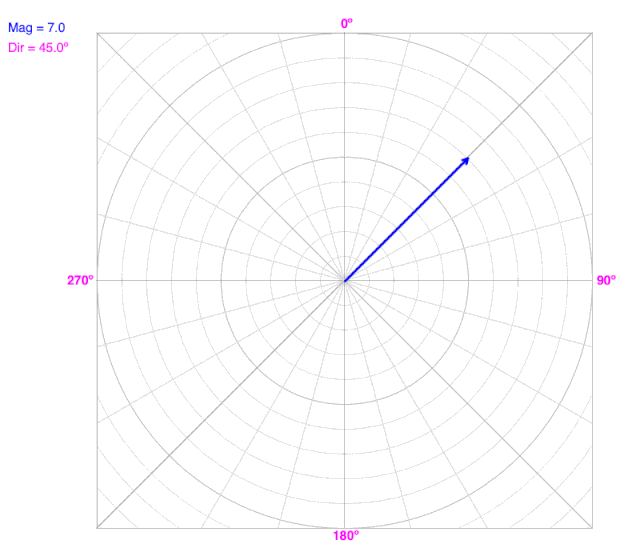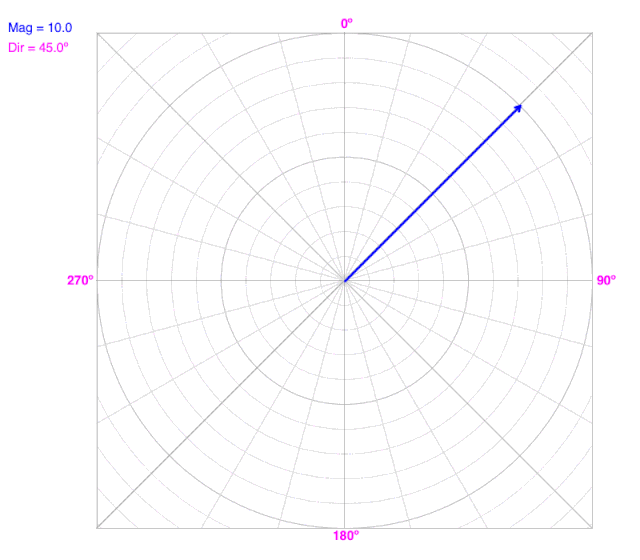
As the radius changes, the line does not change the angle (direction) on a polar coordinate graph.
Modeling Shells in Nature
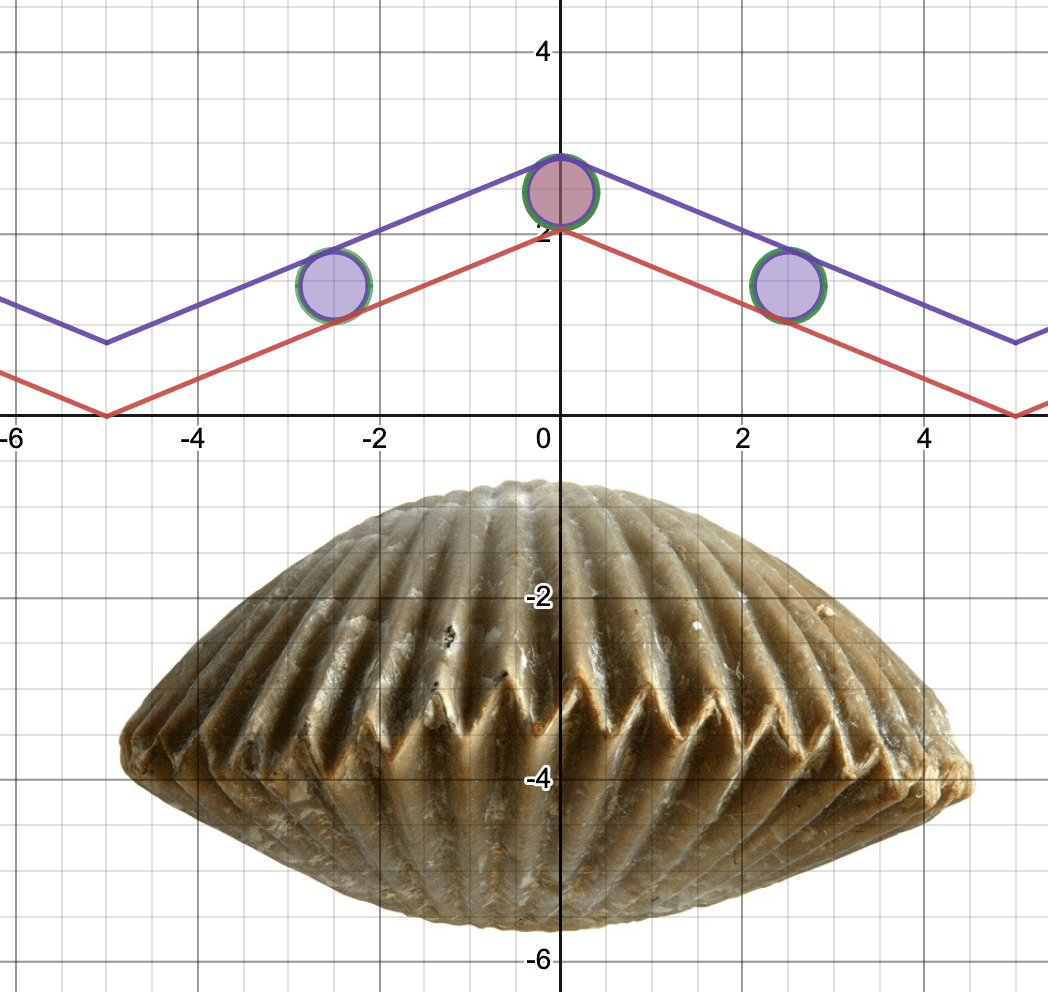
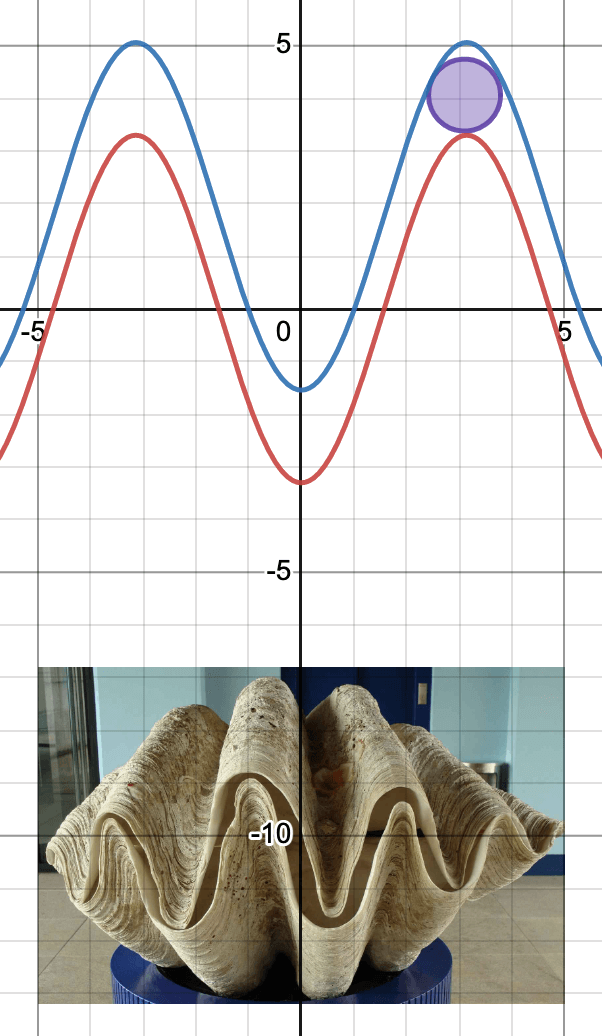
The shape of shells often involves several logarithmic spirals in three dimensions. Some bivalves have straight edges between the two shells, some have crinkly (crenulated) boundaries, and others have wavy ones. Scientists study current and fossil shell morphologies to understand what benefits of surviving in different environments. It turns out wavy and crenulated shell boundaries allow the filter-feeding animals to open their shells a small amount, so larger sediments can’t enter the shell while maximizing how much water can enter for feeding on plankton. Since high energy environments (waves or strong currents) kick up larger sediment into the water, crenulated and possibly wavy shells tend to be found here.
Click on the screenshots of the two models to explore which is better for blocking out sediments while allowing plenty of water to enter the shells.
Open the crenulated shell model by clicking on the graph or clicking here.
Open the wavy shell model by clicking on the graph or clicking here.
This is an exploration activity, but hopefully, it will help you consider the breadth of applying math models to study phenomena to you.