Circles, Ellipses, and Hyperbolas Activity
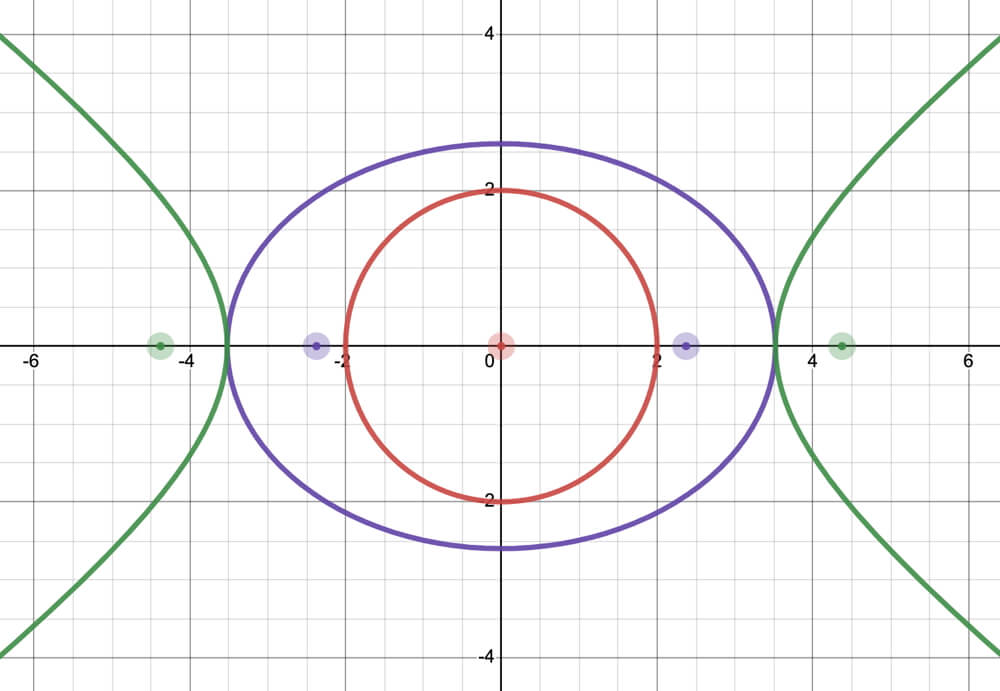
Click on the graph on the right to open the activity to explore circles (red), ellipses (purple), and hyperbolas (green).
Explore circles, ellipses, and hyperbolas as you change the variables h, k, and r, and for ellipses and hyperbolas, a and b. Record your observations in your notebook and compare notes with your peers.
The focus of a circle is its center point (red dot). For an ellipse, foci (purple dots) are the two points used to draw ellipses by hand. Like the ellipse, the summed distance between the two foci (green dots) and a point on the hyperbola is a constant.
After you are comfortable anticipating the behavior as you change the variables, then determine mathematically why:
- h and k result in moving the shapes around the graph,
- r changes the size of the shapes, and
- a and b change the position of the foci and the shapes of the ellipses and hyperbolas.
Open the activity by clicking on the graph or click here.
If you plan on doing more Desmos activities, create a free account on Desmos. Then copy for each model by making a copy and renaming the activity. Tip: make a name that captures what you will explore using the model.
Note: this activity is designed to use a model already created in Desmos. Look at how the equations written on the left create the graphics displayed on the right. The equations look like those we typically see in math textbooks, making using Desmos relatively straightforward.
The Math of Circles
A circle is made up of the points that are equidistant from the center. This means we can use the Pythagorean Theorem where we will use the radius (r) as the distance from the center. Let any point on the circle is defined as (x, y) and the circle’s center is (h, k). A right triangle is created because we use the x and y coordinate system.
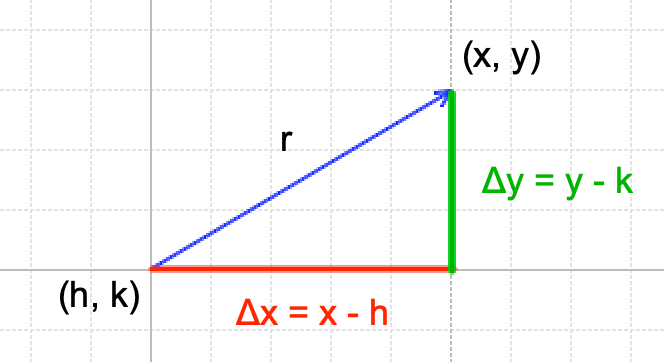
The hypotenuse = radius
Δx = x – h
Δy = y – k
Using the Pythagorean Theorem,
Δx² + Δy² = r²
Substituting,
(x-h)² + (y-k)² = r²
This matches the equation of the circle shown in Desmos.
So h is the horizontal position of the center of the circle, and k the vertical position, and r is the radius of the circle.
Compare the math of ellipses and hyperbolas to that of the circle. Use the equations shown in Desmos to view each.
Common Uses
Circles, ellipses, and hyperbolas (all part of conic sections) are common in our everyday world. Occasionally, someone tries one of the shapes in a situation typically reserved for another shape. For example, the elliptical bike sprocket is becoming common on bikes, whereas circular sprockets were the norm a decade or two ago.
In addition to mechanical devices, consider the importance of reflective conic sections. Explore the reflection of light inside an ellipse here. This is an introduction to dealing with complex mathematical scenarios in an online setting; we often need approximate the calculations to make it easier to program or run faster.
Does it make it easier to conceptualize the uses of circles, ellipses, and hyperbolas after you explored their behavior and looked at the math using the model?