Vectors and Classical Mechanics
Introduction
Classical mechanics is the branch of physics that studies how bodies move, and our understanding helps us analyze and predict the movement of objects on Earth and in our solar system, galaxy, and the universe. The motion of an object requires that we know its position at any given point in time, which means vectors are essential for mathematically calculating movement since direction and magnitude are vital to know.
Conceptually Understanding Movement
Although there are mathematical equations and calculations that follow, conceptually understanding how and why things move are critical to apply physics correctly. We will be using the free simulations and virtual experiments at Advanced Tools for e-Learning to explore the physics of moving objects.
We will be building from the following:
- fundamentals of vectors (magnitude, direction, and axial components) and
- vector addition.
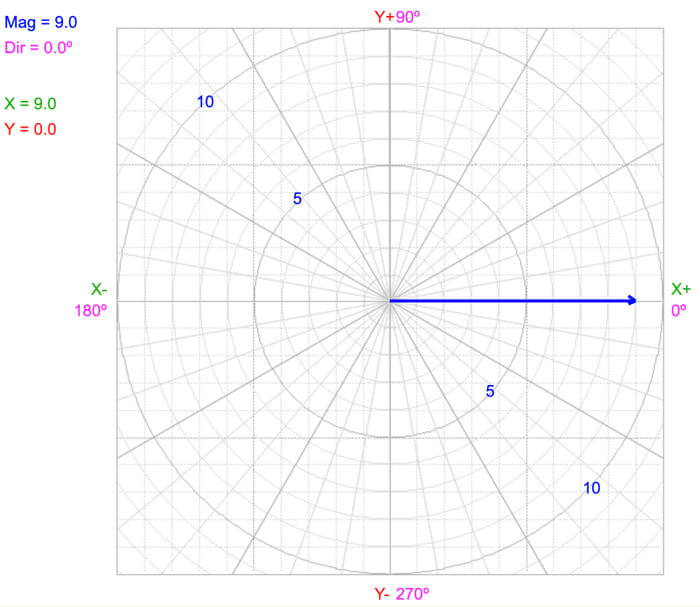
A vector’s direction is relative to axes used to map the space. In this case, +x points to the right, and -x points to the left. In two dimensions, we also use the angle from a selected 0º direction. In this case, we used the convention used in trigonometry, where 0º points in the +x axis.
Kinematics
Kinematics studies the patterns of how things move. The following variables create the mathematical structure for describing motion:
- Position is the place where something is located within a mapped space, and for the following, we’ll label it as x.
- Displacement (△x) is the change in position of an object:
△x = x1 – x0
Note that Δx may be positive or negative, which indicates direction relative to the x-axis.
- Velocity (v) describes how displacement changes with time:
v = △x / △t = (x1 – x0) / (t1 – t0)
Where △t is the change in time that the motion was observed, and the subscripts denote when and where the object was observed.
- Acceleration measures how velocity is changing over time:
a = △v / △t = (v1 – v0) / (t1 – t0)
These relationships lead to four key kinematic equations for objects moving at constant acceleration:
△x = (vi + vf) / 2 * t
△x = vi * t + 0.5 * a * t2
vf = vi + a * t
vf2 = vi2 + 2 * a * △x
Where t is the time since the observing the motion began, vi the initial velocity, and vf the final velocity (or that observed at time t).
Explore how these equations are derived from the velocity vs. time graph.
Dynamics
Dynamics focuses on why things move, and this means we study forces that create a change in motion, which is also known as acceleration.
The acceleration of an object is equal to the force acting on an object divided by the mass of the object, or rewritten as F = ma.
Since the kinematic equations above describe the motion of objects moving with constant acceleration, this means that the force(s) acting on the object must remain constant as well. Objects moving with constant acceleration are the simplest to work with, helping us to understand the more complex movement of water and air on Earth, which are not moving at a constant acceleration.
Graphing Motion
Graphing how an object’s position and velocity change over time helps show how an object is accelerating.
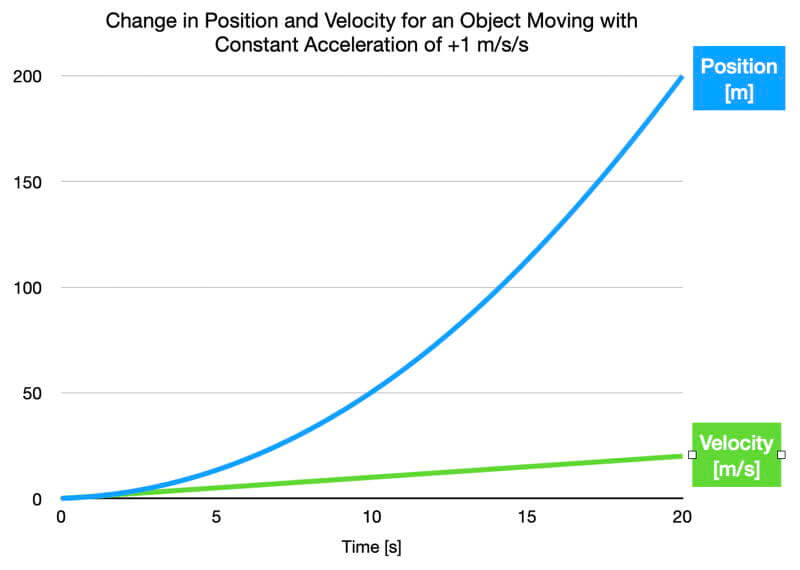
Graph of the position and velocity with time for an object accelerating at a constant +1m/s². This means the object is accelerating in the direction the object is moving. Notice how the velocity increases linearly with time, and the change in position increases exponentially with time.
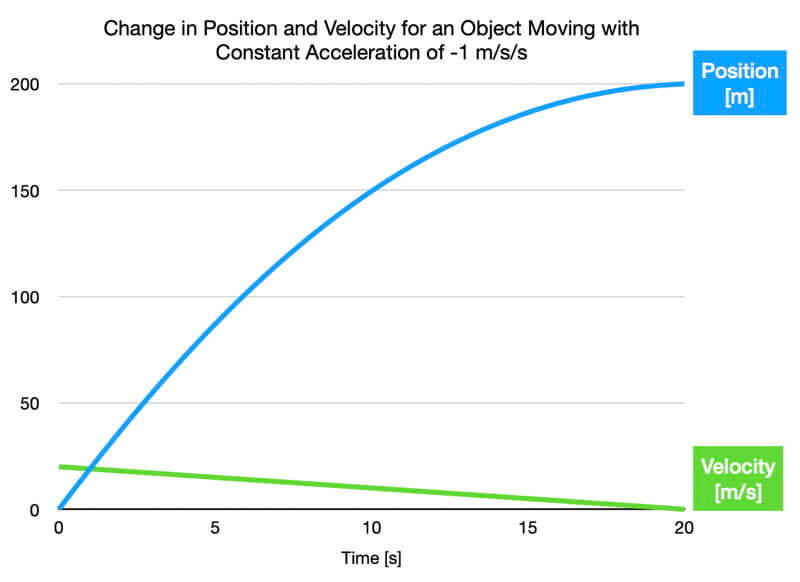
Graph of the position and velocity with time for an object accelerating at a constant -1m/s². In this scenario, the acceleration opposes the direction the object is moving in. Notice how the velocity decreases linearly with time, and the change in position slows exponentially with time.
If the object continues moving after 20 seconds, the object will begin moving toward the starting point, and velocity would become negative.
Applying Classical Mechanics to Golf
Using Resources at Advanced Tools for e-Learning (ATeL)
ATeL has created a folder of their free activities that support Science Pickle*, which includes a variety of activities to study one- and two-dimensional motion in the context of the game of golf:
- Simulations let you explore how the many moving parts of a complex process fit together. In these simulations, explore how position, velocity, acceleration, and forces are involved in putting (straight-line motion in one-dimension when putting horizontally, and two-dimensional motion when the green is slanted) and chipping a golf ball (two-dimensional motion through the air).
- Virtual experiments guide you through an investigation.
- Lessons that define and illustrate concepts as needed.
- Assessments allow you to check your knowledge and understanding.
- A wizard-driven authoring tool enables you to modify existing virtual experiments and assessments and create new ones. Teachers may design activities tailored for their classes, and learners may use the tool to prepare for a test.
* There are many more topics available to explore at ATeL’s website. Register to get access to their free activities.
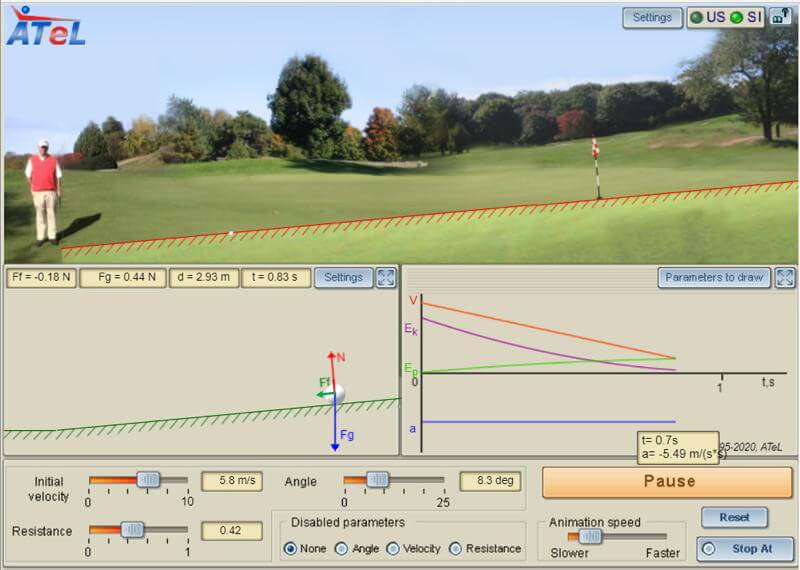
Screenshot of the putting simulation that shows a range of data viewing options. View the velocity, force, and acceleration vectors as the ball travels along the green. If you are familiar with the Work-Energy Theorem, potential energy, and the conversation of energy you may also view the kinetic, potential, and total mechanical energy of the moving golf ball.
Force of Gravity (Fg) or Weight
Bodies of mass gravitationally attract each other with force proportional to the mass of each object and inversely proportional to the square of the distance between their centers.
Force of gravity = Fg = G * m1 * m2 / d2
where G = gravitational constant,
m1 = mass of the first object,
m2 = mass of the second object, and
d = distance between the centers of the two objects.
If a body is on the Earth’s surface (or relatively close to it), then let m1 = mass of the Earth (mEarth), m2 = mass of the body of interest, and d = radius of the Earth (RadiusEarth).
Since F = m * a, then
Fg = m * ag = m * G * mEarth / RadiusEarth2
Therefore, ag = G * mEarth / RadiusEarth2 = 9.8 m/s² = “g” in most textbooks.
The force of gravity acting on a body at or near the Earth’s surface is commonly called the object’s weight, which we’ve just shown is
Fg = weight = m * g
The weight of the golf ball points toward the center of the Earth.
CAUTION: It is essential to recognize when “m” is referring to mass or a unit of length when working in physics (or chemistry).
Normal Force (FN)
The normal force is the component of a contact force that is always perpendicular to the surface that an object contacts. Both objects may be solids, but they don’t have to be. In this case, the solid ground pushes perpendicular against the surface of contact with the golf ball. If the green is horizontal, the atoms that make up the ground create a barrier for the ball to move due to the force of gravity.
Note: the term “normal” has many meanings. In this usage, “normal” means “perpendicular.” The contact force between the two objects is perpendicular to the surface of contact.
Friction (Ffr)
Friction is the component of a contact force that is always parallel to the surface of contact. Friction opposes motion. If the object is not moving, static friction opposes any force trying to push it along the surface. If the body is sliding, kinetic friction acts in the direction opposing the motion. In most cases, friction is independent of the contact’s surface area and is proportional to the normal force.
Force of friction = Ffr = μ * FN
where μ is the coefficient of friction.
The coefficient of friction depends on the roughness of both surfaces that are in contact. When both bodies are stationary to each other, μ is called the coefficient of static friction (μs). When one body is sliding along the surface of the other, μ is called the coefficient of kinetic friction (μk), and the value is independent of the speed of the sliding.
Note: μk ≤ μs
The coefficient of friction of golf greens changes throughout the day as the grass grows and as the amount of moisture in the blades dries in the intense afternoon sun.
Air Resistance (Far)
Air resistance is similar to friction in that it always opposes the motion of an object. But unlike friction, its magnitude depends on the speed of the object moving through the air. The faster an object moves, the higher the air resistance. The magnitude also depends on the cross-sectional area relative to the motion. A skydiver slows down by spreading themselves out perpendicular to their motion, and speed up by falling head first.
Putting: Straight-Line Motion
Forces Acting on a Putted Golf Ball
This simulation does not deal with how the golf ball got moving. Instead, it is about what happens to the ball once it leaves the putter and moves across the green. Three forces act on the moving ball:
- the force of gravity (mg) pulling the ball toward the center of the Earth,
- the normal force (FN) of the ground (green hashed surface) pushing perpendicularly on the ball, and
- the force of friction (Ffr) between the surface of the golf ball and the land. Friction always acts parallel to the surface of contact and opposes the direction of motion.
If the green is slanted, the weight of the ball has components of force parallel and perpendicular to the surface.
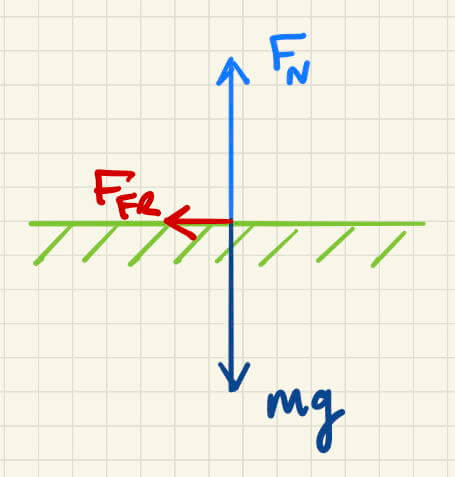
An illustration of the forces acting on a golf ball once putted on a horizontal surface (hashed green lines). Since the ball is not leaving the surface, the normal force must equal the weight of the ball so the forces are balanced in the vertical direction. Since there is only one force acting in the horizontal direction, the ball must be accelerating in the direction of the friction, which is always opposite the motion of the ball.
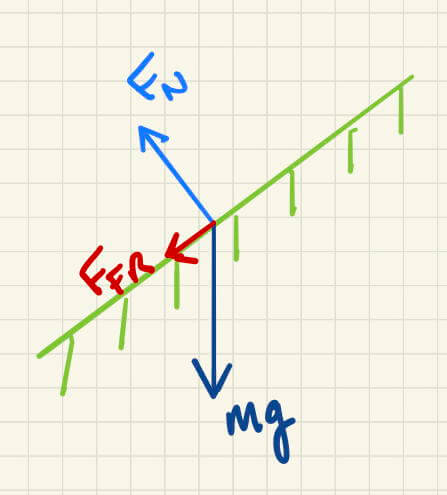
An illustration of the forces acting on a golf ball once putted up a slanted surface (hashed green lines). Since the ball is not leaving the surface, the normal force must equal the component of the weight of the ball that is perpendicular to the surface, so the forces are balanced. The component of weight parallel to the green increases the net force opposing the moving ball, so the ball won’t roll as far compared to when putted on a horizontal green.
Simulations may be used to run experiments as if you had the equipment and were on a golf course. Try the following:
Keeping all other variables constant, how much farther will the ball travel when the initial velocity is doubled?
Regardless of the slope of the green, the ball travels four times as far when the initial velocity is doubled.
Challenge: Prove this relationship using
vf2 = vi2 + 2 * a * △x
Where a is the acceleration acting parallel to the putting green.
Tip #1: vf = 0.
Tip #2: The acceleration acting on the ball parallel to the putting green is independent of the speed of the ball.
On a horizontal green, how much farther will the ball travel when the coefficient of kinetic friction is doubled?
The ball travels half as far when the coefficient of kinetic friction is doubled.
Challenge: Prove this relationship using
Ffr = μk * FN = m * a
and
vf2 = vi2 + 2 * a * △x
Where a is the acceleration acting parallel to the putting green and m is the mass of the golf ball.
Tip: FN = m * g on a horizontal green.
NOTE: If μk = 0, the moving ball would never stop! This is why the simulation won’t run with the setting.
Chipping: Motion in Two Dimensions
Forces Acting on a Golf Ball Moving Through the Air
Unlike putting on a flat green, a golf ball moving through the air changes direction. Breaking up the movement into vertical and horizontal components allows us to apply the kinematic equations in each direction.
The force of gravity is always acting vertically downward on the ball as it moves through the air. If the ball is moving upward, gravity is slowing its rate of ascent, but once it begins to fall back to Earth, the ball accelerates downward.
When there is air resistance, the acceleration of the golf ball is not constant because the forces acting on the ball are continually changing. Air resistance always opposes the motion of the golf ball, and its magnitude depends on the velocity of the ball.
If air resistance is not present, how does the starting velocity compare to velocity when it lands?
The golf ball has the same magnitude of the velocity (speed) as it lands is the same as when it left the ground. The angle relative to the ground is also identical. If the ball leaves the ground at 50º, then it lands at 50º to the ground.
Notice that the trajectory is symmetric about the peak height of its journey through the air. The velocity in the horizontal direction remains constant, but the vertical velocity changes due to the force of gravity. As the ball rises, gravity decreases the upward velocity, and when the ball descends, gravity increases the downward velocity.
If air resistance is included, how does the starting velocity compare to the velocity when it lands if there is no wind?
The golf ball is moving slower when it lands than when it left the ground. The angle relative to the ground is also different. If the ball leaves the ground at 50º, then it lands at an angle larger than 50º to the ground.
Notice that the ball’s trajectory is no longer symmetric about the peak height of its journey through the air. The angle of ascent changes more gradually compared to its descent. Recall that air resistance always opposes the motion of the moving golf ball. The horizontal velocity is decreasing throughout its trajectory, but at a decreasing rate since air resistance is greater when the object is moving faster. Vertically, the golf ball doesn’t rise as high compared to no air resistance since it too is affected by air resistance.
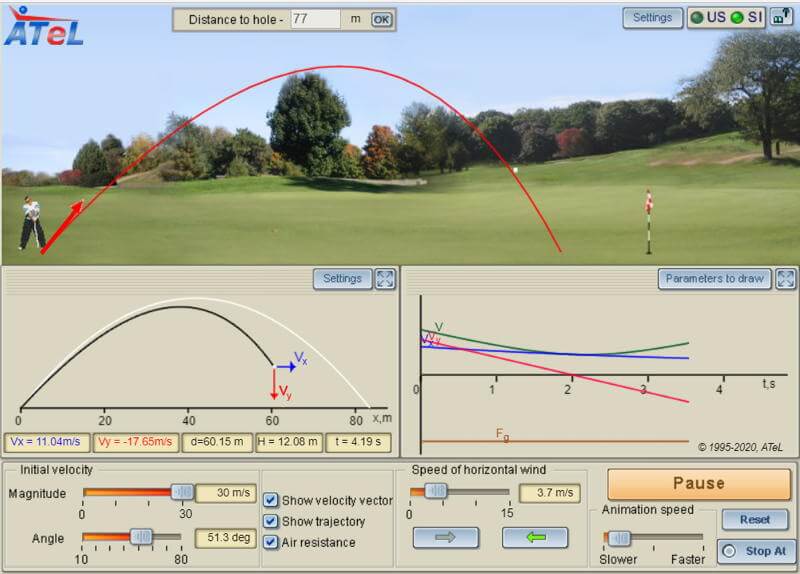
Screenshot of the chipping simulation that shows a range of data viewing options. View the velocity, force, and acceleration vectors as the ball travels through the air. Horizontal and vertical components of the vectors may be viewed as well.

0 Comments