Using Sundials
Humans have been using the Sun’s position to navigate and tell the time, day, and season for millennia. Sundials create shadows that make it easier to do these tasks. In the following sections, explore how to use the simplest sundial (a vertical stick or pole) as a compass, clock, and calendar, then practice with the Sundial Shadow app at the bottom of the page. But there is a catch – how humans use time is often different than how nature responds to the Sun’s motion during the day and throughout the year! Clock time that humans use does not equal solar time that nature responds to.
Human Use of Time and a Calendar
is different than
Nature’s Response to Time and Season
Since this topic is part of the Earth Systems course, we will focus on using the position of the Sun in the sky to examine nature’s behavior. However, this information is useful for humans to understand and apply for our needs, particularly designing energy-efficient and aesthetically pleasing buildings, collecting energy with solar panels, all aspects of farming, and quite a bit in our outdoor recreation.

Above is an example of using a vertical pole to track the movement of shadows throughout the day. Use color string to show the position of shadows at different times of the day and a different color to connect the tips of the shadows to visualize how the shadows have changed during the day. See A Sundial as a Clock, Compass, and Calendar.
Explore First?
Explore how shadows move during the day at different locations and seasons with the web app, Sundial Shadows. Look for patterns and trends, then explore the science behind it; dive into the science first, then reinforce your understanding with the app; or go back and forth between the two. The key is to try to answer your questions and make sense of your observations.
The Sundial Shadow App
Use the Sundial Shadows web app to visualize, conceptualize, estimate, and use shadows and shadow traces as a clock, calendar, and compass. View the shadows for any latitude, day, and time, and try the unlimited number of challenges that provide visual feedback based on your answers. The app created the diagrams and animations of sundial shadows on this page.
Earn a Certificate
Answer ten random challenges to earn a certificate to gauge your understanding. Use as a homework assignment, or earn points and clues on the final Earth Systems challenge (when it gets completed): you must identify the best place to inhabit a new planet that you have traveled to. Try as often as you like to earn the most points.
Acknowledgments
I would like to thank Lincoln Berkley, Mattea Horne, Kiley Remiszewski, and Tom Whittaker for sharing their insightful questions, comments, and suggestions to improve the app.
Explore the Math
For a well-written and illustrated review of the math of sun shadows, see Solar Geometry.
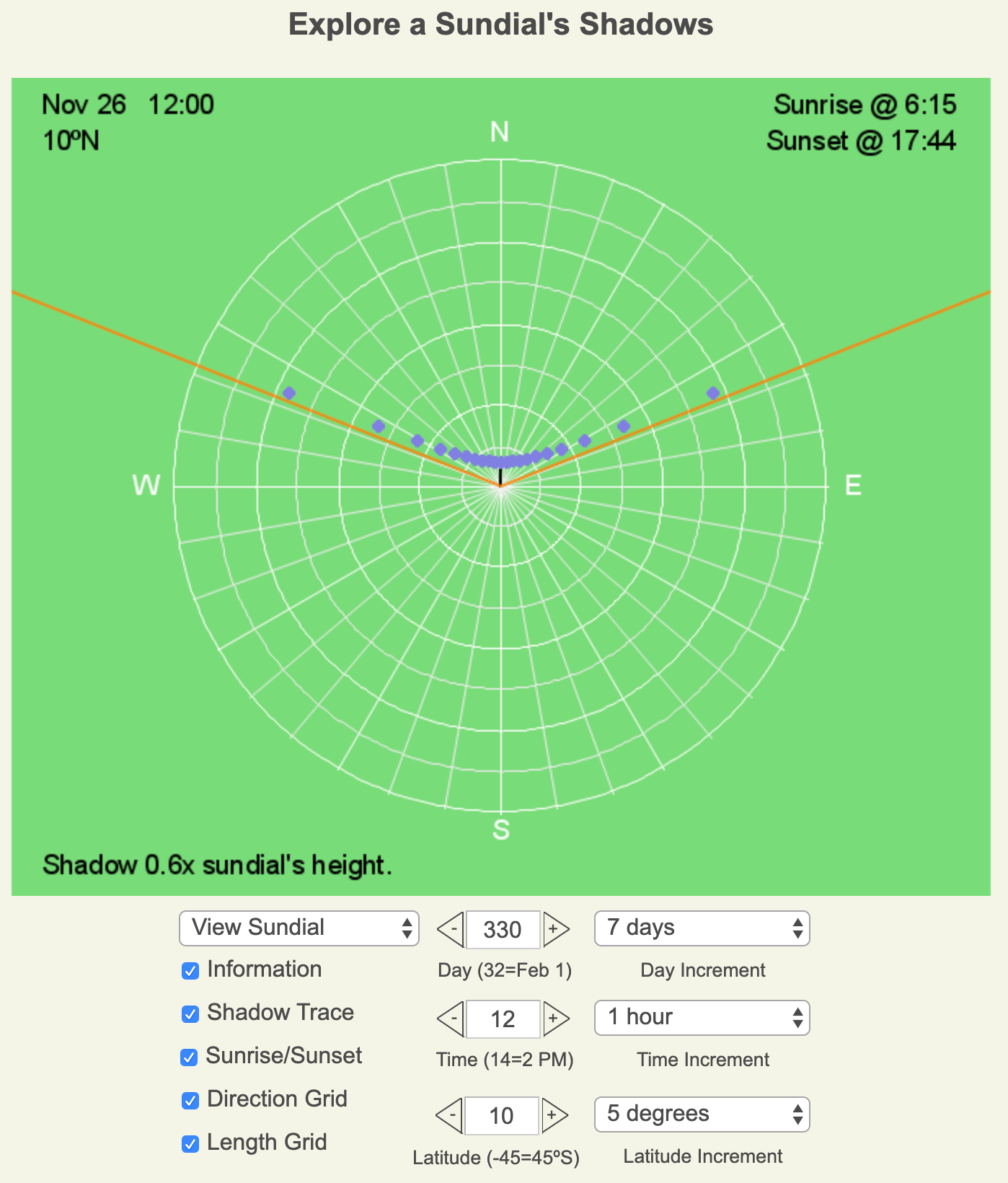
Above is a screenshot of the Sundial Shadows’ interface. The blue dots are the tips of the sundial’s shadow every 30 minutes, the block line is the sundial shadow for the displayed time of day, and the orange lines are the shadows cast at sunrise and sunset.
Example Challenges
Below are examples of the three categories of challenges. To answer on the app, click the white box with the correct answer.
Latitude Challenge
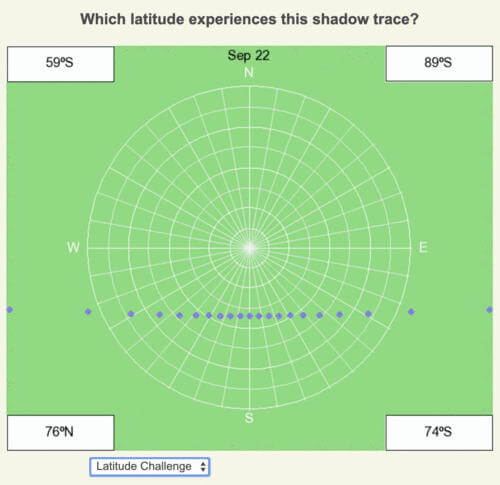
Reasoning and Answer
September 22 is within a day of the equinox, hence the minimal curvature of the shadow trace. At local noon, the shadow is pointing south, so it is in the Southern Hemisphere. The shadow length is just over 3x longer than the sundial’s height, which means the local noon sun angle is less than 18º above the horizon (see the data table above). The latitude must be greater than 90º – 18º or 72º S, which means the answer is 74ºS.
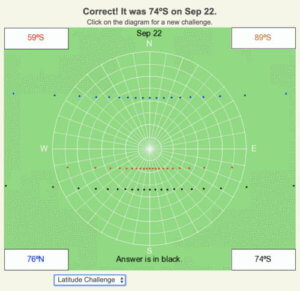
The correct answer, 74ºS, is in black, and the shadow traces of the possible incorrect answers are color-coded.
Time Challenge
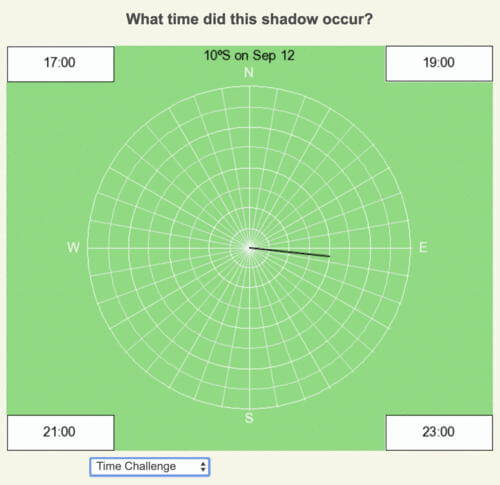
Reasoning and Answer
This day is close to the equinox, so there is minimal curvature of the shadow trace. At 10º away from the equator, the amount of daylight will be close to 12 hours throughout the year. The shadow is well east of the local noon position, so it is well after noon time. The only time that meets these criteria is 5 PM (17:00). The other times of the day are below the horizon.
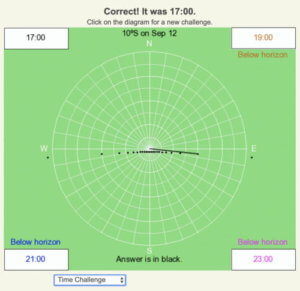
The correct answer is in black, and the shadows of the possible incorrect answers are color-coded.
Day Challenge
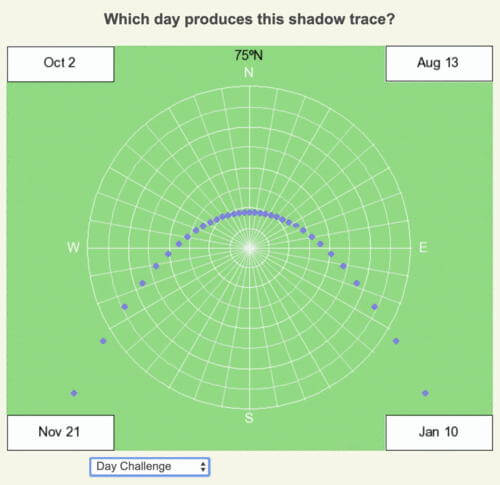
Reasoning and Answer
The shadow trace curves quite a bit, so the day is close to a solstice. Since the shadows at sunrise and sunset are well south, the Sun is rising well north of east and setting well north of west. Therefore the solar declination must be positive. The location is well north of the Arctic Circle (66.5ºN), so close to the June 21 solstice, there won’t be a sunset, and the shadow trace would be elliptical. That means the date is between June 21 and September 21. August 13 fits these criteria.
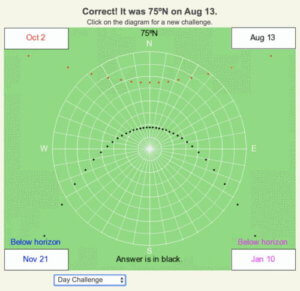
The correct answer is in black, and the shadows of the possible incorrect answers are color-coded.
Brief History of Sundials
Humans are planners and organizers. Since the Sun’s diurnal and seasonal heating of the Earth’s surface creates cyclical patterns in nature, humans invented technologies to understand, track, and predict these patterns. Artifacts indicate humans have been tracking solar patterns as early as 20,000 years ago. By 5,500 years ago, vertical sticks and stones cast shadows that showed solar time and season of the year. To support growing the needs of communities, trade, and farming, Babylonians and Egyptians refined the process with more advanced sundials. The unified process to tell time helped organize societies’ activities.
As sundial technology advanced, and identifying time became more precise, humans realized new technologies were needed to support the increasing use in science, commerce, agriculture, navigation at sea, military, global exploration, and industry. The invention of mechanical clocks created a technology that better supports human needs. Yet, it created a diversion from tracking and understanding one of the most fundamental drivers of nature: the Sun illumination of Earth. Most humans today, especially those living in cities, are not aware of solar time (the time based on the Sun’s movement). Instead, we rely entirely on the time told by clocks.

One of the advancements in sundials was tilting the gnomon (the stick or edge that casts the shadow) to point toward the celestial pole. This modification makes the gnomon parallel to the Earth’s axis of rotation and allows for one set of time markings to be used throughout the year. A vertical gnomon requires a series of markings to tell the time and day of the year.
Sun Time versus Clock Time
Clocks standardized time for human use, and as time-monitoring technologies advanced, human reliance on nature’s patterns lessened. Before railroads, towns and cities had their unique reference for clock time that relied somewhat on the timing of local noon. However, to coordinate the rapid speeds and long distances of railroad travel required unification of time across broader regions. By 1883, the United States created four time zones across the country, and one year later, the international community divided the world into 24 time zones.
Each time zone is roughly 15º in longitude wide, which means solar time differs by 1 hour between the eastern and western edges of the zone. Live along the east border, and you experience sunrise and sunset one hour earlier, clock time, than a person living on the western side of this time zone.
To add complication to the difference between a clock and solar time, the Earth’s orbital speed changes throughout the year since its orbit is not perfectly circular (see the section on eccentricity). A solar day is the time difference between two successive local noons. If the Earth is moving faster in its orbit, it must rotate more to align with the next day’s local noon, so the day is longer when recorded by a clock. When Earth moves slower, the solar day is shorter. The Equation of Time allows humans to account for the difference between a clock and solar time.
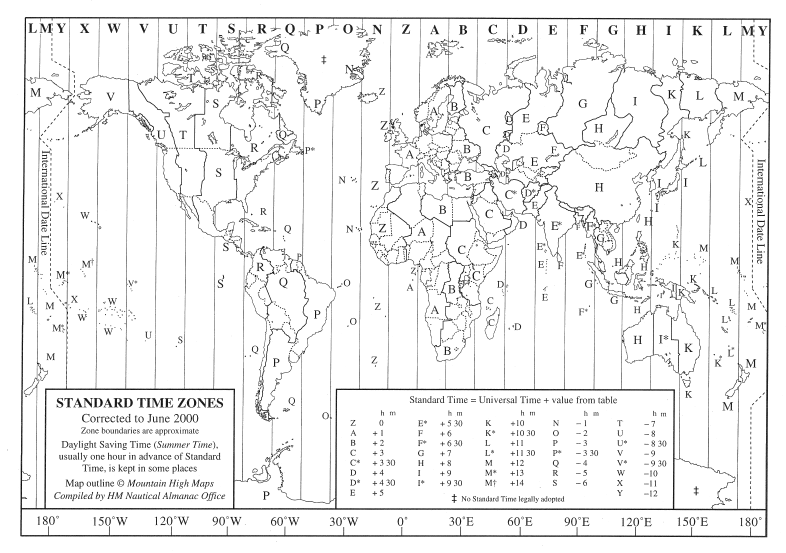
Map of time zones across the globe. Time zones are roughly 15º longitude wide since the Sun appears to move across the sky at 15º longitude per hour. Clocks within a time zone all have the same time. The image is from http://www.travel-images.com/time-zones.html.
Using Declination Circles to Calculate Shadows
Declination circles map the path of the Sun across the sky as viewed from a point on the Earth’s surface at a given latitude and day of the year. A sundial located at this point extends above the surface, so it creates a shadow. The tip of the shadow points away from the Sun and changes location on the ground throughout the day. The shape of the shadow trace (the connected tips of the shadows throughout the day) ranges from a circle, ellipse, parabola, and line, whereas the declination circle is always a circle. The observed shadow’s pattern has a different shape than the declination circle except at the North and South Poles when the sun is above the horizon.
The three views of the declination circle shown below are the position of the Sun in the sky during January 1 at 45ºN. The yellow lines show the hourly beams of sunlight hitting the Earth’s surface and the tip of a sundial. Its altitude above the horizon and hour angle identifies the position of the Sun in the sky. The hour angle is zero at local noon, which is when the Sun is highest in the sky as it crosses the local longitude. Before local noon, the hour angle is negative, and after local noon, the hour angle is positive. Use the horizontal gray lines that are 10º apart to interpolate the altitude of the Sun. Use the vertical arcs that are 10º apart to calculate the hour angle.
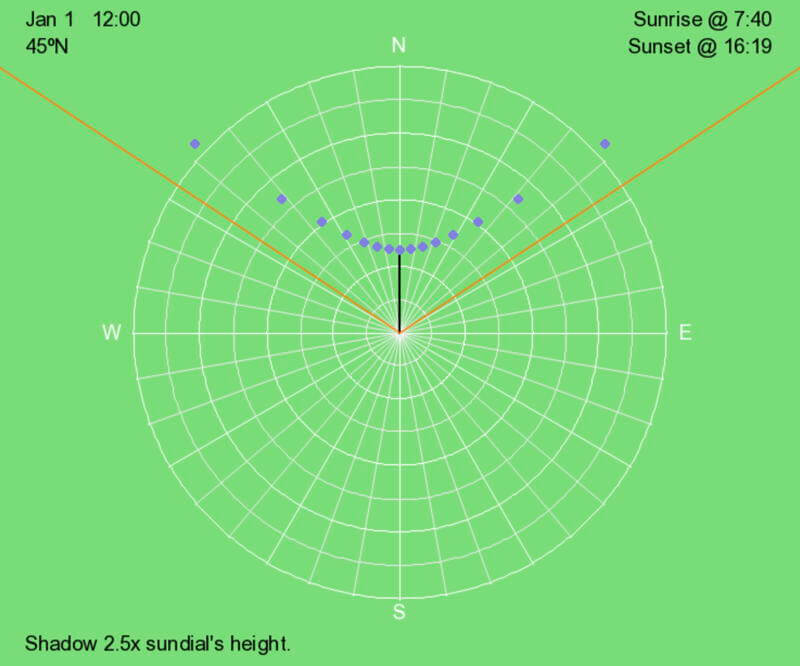
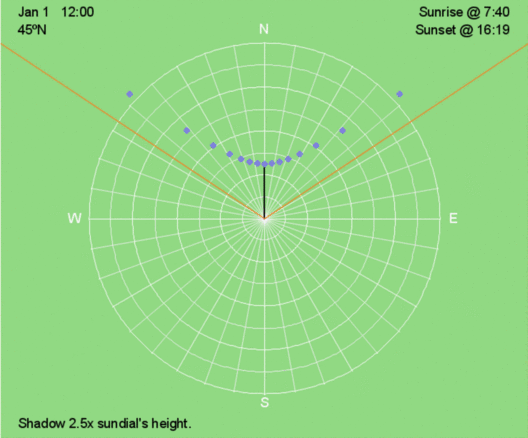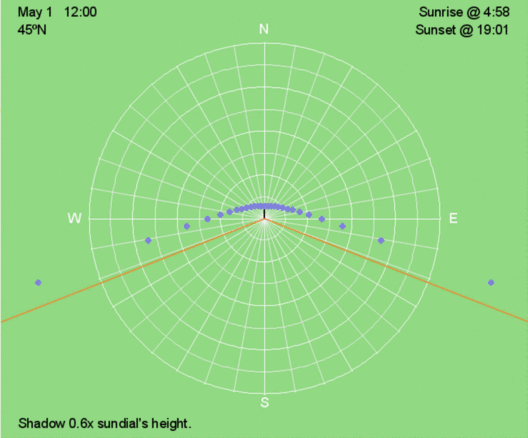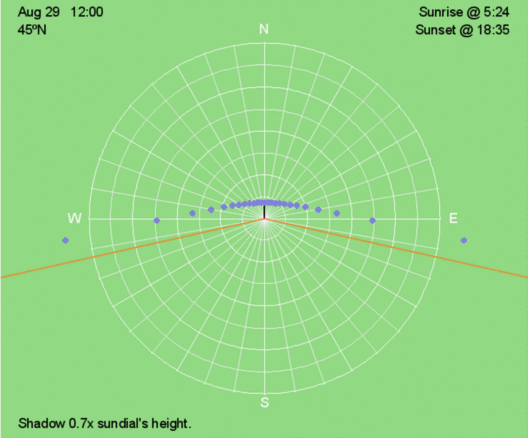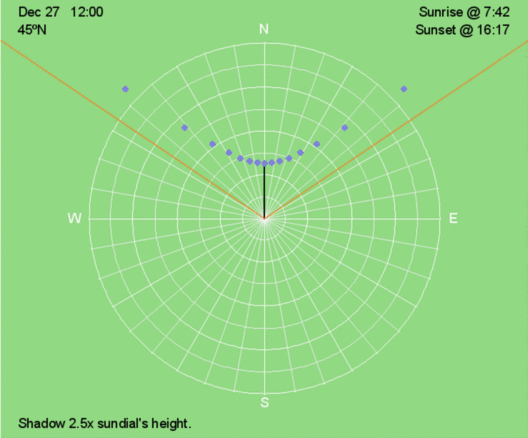
Shadows point away from the Sun. In the illustration above, the blue dots represent the tips of a sundial’s shadow every 30 minutes on January 1 at 45ºN. The orange lines show the shadows at sunrise and sunset. The black line is the shadow at local noon.
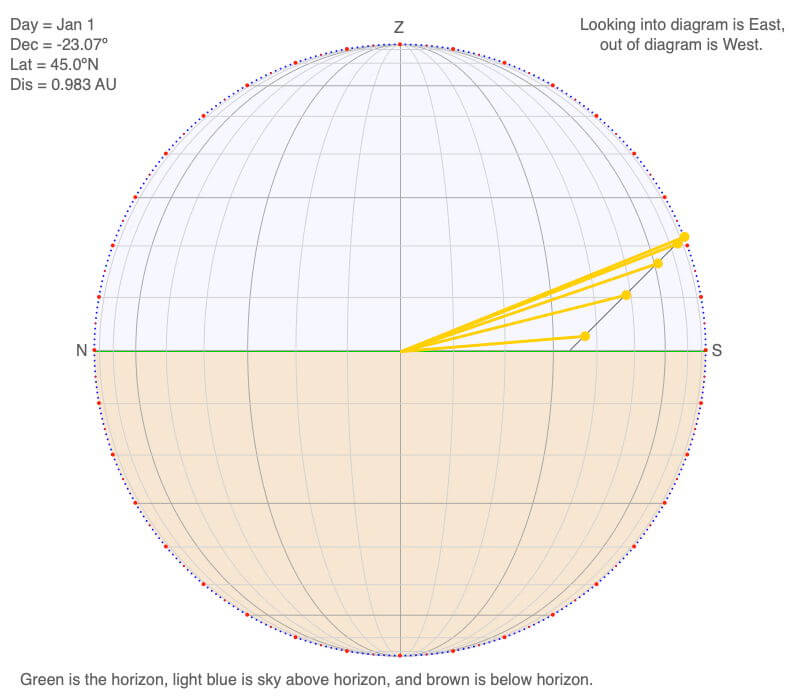
Above is the north-south oriented view of the declination circle for January 1 at 45ºN. The yellow circles represent the hourly position of the Sun, and the yellow lines represent the hourly beam of sunlight illuminating the center of the horizon.
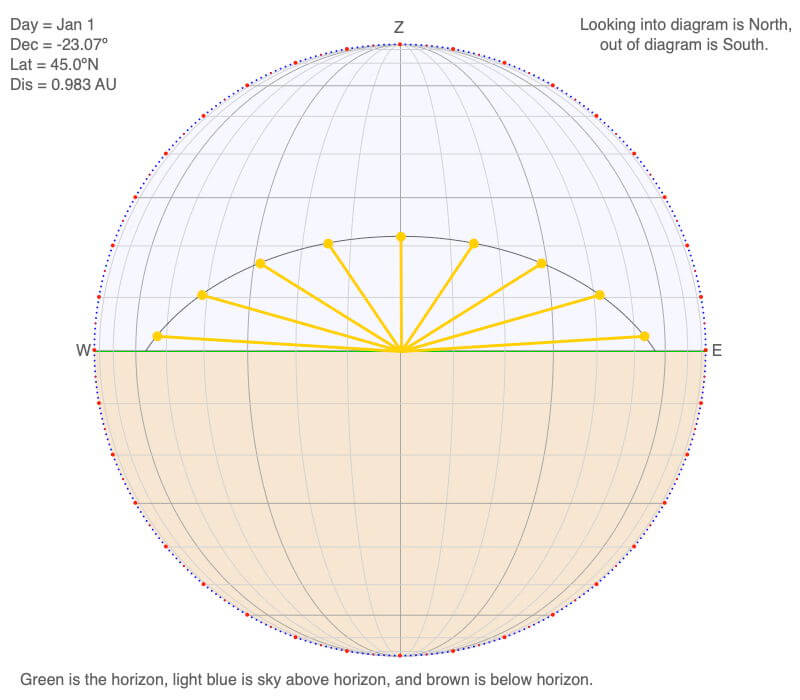
Above is the east-west oriented view of the declination circle for January 1 at 45ºN. The yellow circles represent the hourly position of the Sun, and the yellow lines represent the hourly beam of sunlight illuminating the center of the horizon.
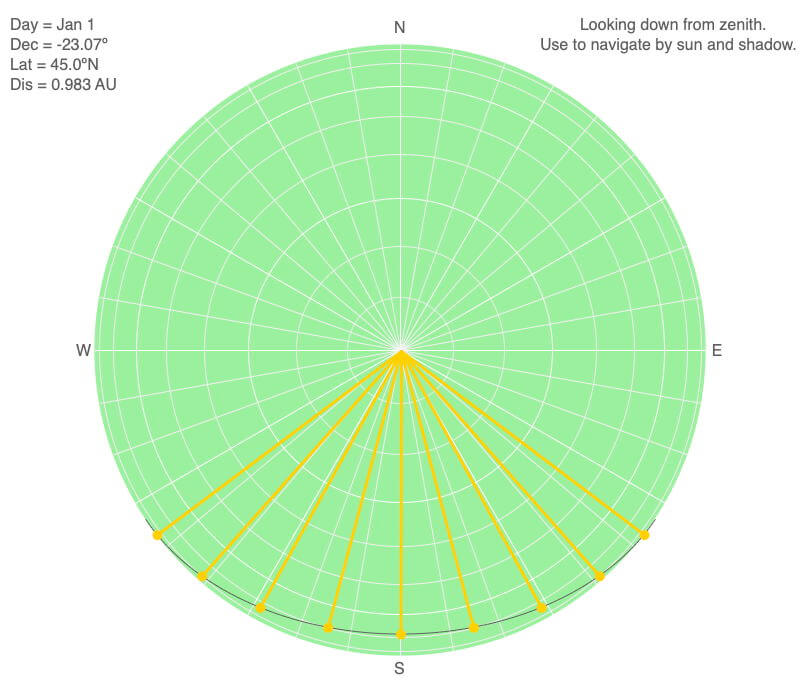
Above is the map view of the declination circle for 45ºN on January 1, which is ten days after the December 21 solstice. Hence, the southern hemisphere is considerably more illuminated than the northern hemisphere. The Sun rises roughly 37º south of east, which produces a shadow 37º north of west. The Sun sets 37º south of west, creating a shadow 37º north of east.
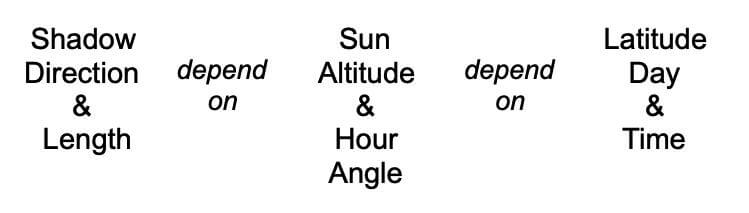
Shadows & Sun Position Depend on Latitude, Day, & Time
Shadows point away from the Sun, and the position of the Sun in the sky means applying declination circles and how they involve latitude, day, and time. Therefore shadow length and direction depend on the latitude, day, and time.
When a variable depends on several variables, there is a dependency between each variable to the others. For example, to calculate the area of a rectangle, multiply the width and length. If the area and the width are known, then the length may be calculated by dividing the area by the width. Similarly, if we know the latitude, day, and time, shadow length and direction may be calculated. If the shadow and two of the variables latitude, day, and time are known, then the third may be calculated. This flexibility is how we use shadows as a compass, clock, and calendar.
In the animations and illustrations that follow, the blue dots represent the tips of a sundial’s shadow every 30 minutes. The set of blue dots represents the shadow trace. The orange lines show the shadow at sunrise and sunset. The black line is the shadow at the time displayed in the upper left corner.
The white lines are direction every 10º, and the white circles are the relative length of the shadow compared to the height of the sundial. Use the relative shadow lengths to calculate and/or interpolate the altitude of the Sun above the horizon (see the table on the right).
Table of the relative length of the shadow and the altitude of the Sun in the sky.
| Relative Length of the Shadow | Altitude of the Sun Above the Horizon |
| 0x | 90º |
| 1x | 45.0º |
| 2x | 27.0º |
| 3x | 18.43º |
| 4x | 14.0º |
| 5x | 11.3º |
| 6x | 9.5º |
| 7x | 8.1º |
| 8x | 7.1º |
Using the Sun and Shadows as a Compass
The first step is to become familiar with how shadows change across the globe with the season. Below are animations of shadow traces for three seasons: December 21, when the Northern Hemisphere is most illuminated; an equinox, when both hemispheres are evenly illuminated; and December 21, when the Southern Hemisphere is most illuminated. Latitude begins at 90ºN and decreases at 15º intervals until it reaches 90ºS.
Local Noon: The Anchor of Our Compass
When the Sun is highest in the sky, it is crossing the local longitude. Lines of longitude are oriented north/south. At local noon, the shadow is either pointing north or south, unless the Sun is directly overhead and there won’t be a shadow.

On December 21, the Sun’s declination is 23.5ºS, so all shadows at sunrise and sunset across the globe are north of east and west, respectively. At and northward of 66.5ºN, the sun remains below the horizon all day. At and south of 66.5ºS, the Sun remains above the horizon all day. Northward of 23.5ºN, the local noon shadow will always point northward. South of 23.5ºS, the local noon shadow will always point southward.
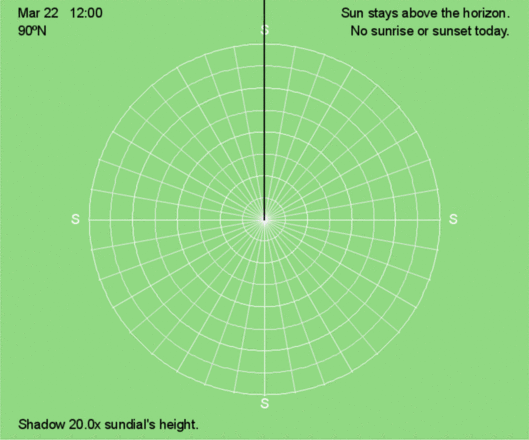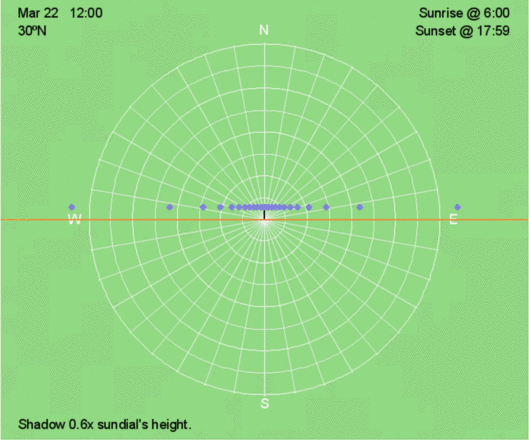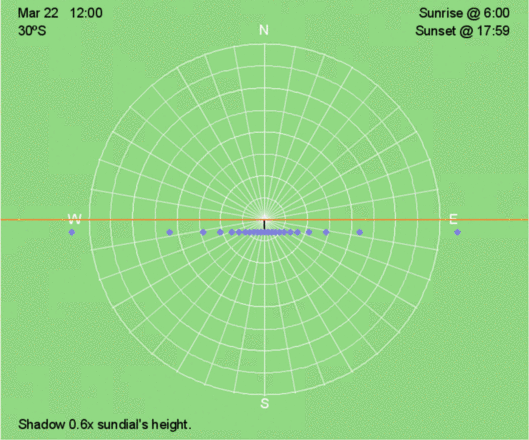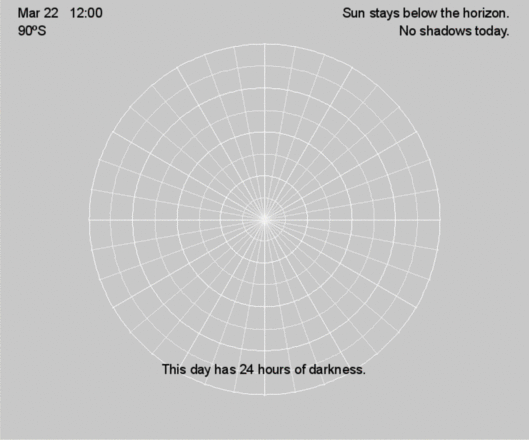
Except for the poles, on the equinoxes, the Sun rises exactly east and sets exactly west at all latitudes, creating 12 hours of sunlight and darkness. At the poles, the Sun remains on the horizon for 24 hours.

Shadows on June 21 are a mirror image of those observed on December 21. The Sun’s declination is now 23.5ºN, so shadows at sunrise and sunset are south of east and west, respectively.
All shadows during the day at latitudes south of 23.5ºN will have a southward component on June 21. Conversely, on December 21, all shadows during the day at latitudes north of 23.5ºS will have a northward component.
Key Patterns of Shadows with Season
- Except at the Poles, shadow traces curve less near the equinoxes (March 21/22 and September 21/22). At the Poles, when the Sun is above the horizon, the shadow trace is circular.
- Near the December 21 solstice, shadow traces curve northward for all latitudes that experience a period of darkness that day. The closer toward the solstice, the more pronounced the curvature.
- Near the June 21 solstice, shadow traces curve southward for all latitudes that experience a period of darkness that day. The closer toward the solstice, the greater the curvature.
- North of 23.5ºN, the Tropic of Cancer, the shadow at local noon always points north. The shadows are longer near December 21 compared to those near June 21.
- South of 23.5ºS, the Tropic of Capricorn, the shadow at local noon always points south. The shadows are longer near June 21 compared to those near December 21.
- Between the Tropics of Cancer and Capricorn, the Sun is directly overhead at local noon twice a year, so there won’t be a shadow at that time. For these latitudes,
the local noon shadow will point north when Latitude – Declination > 0º
and will point south when Latitude – Declination < 0º
The Sun will be directly overhead when Latitude – Declination = 0º
Recall that southern latitudes are negative, so 10ºS = -10º.
Solar declination is essential for calculating the angle of the local noon sun above the horizon in the Northern Hemisphere:
90º – Latitude + Declination = Local Noon Sun Angle
and for the Southern Hemisphere:
90º + Latitude – Declination = Local Noon Sun Angle
Click to run the Solar Declination web app to practice calculating solar declination from the graph similar to the following.
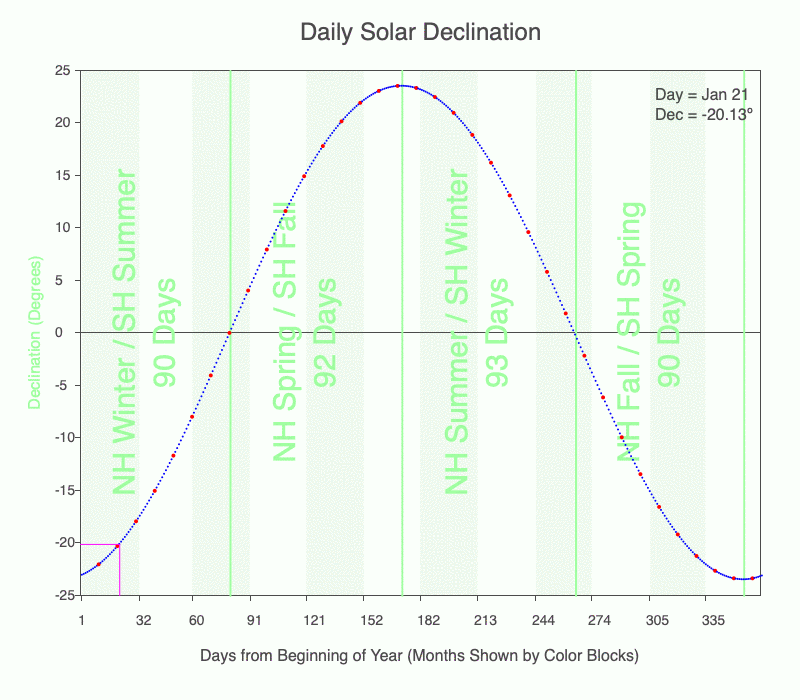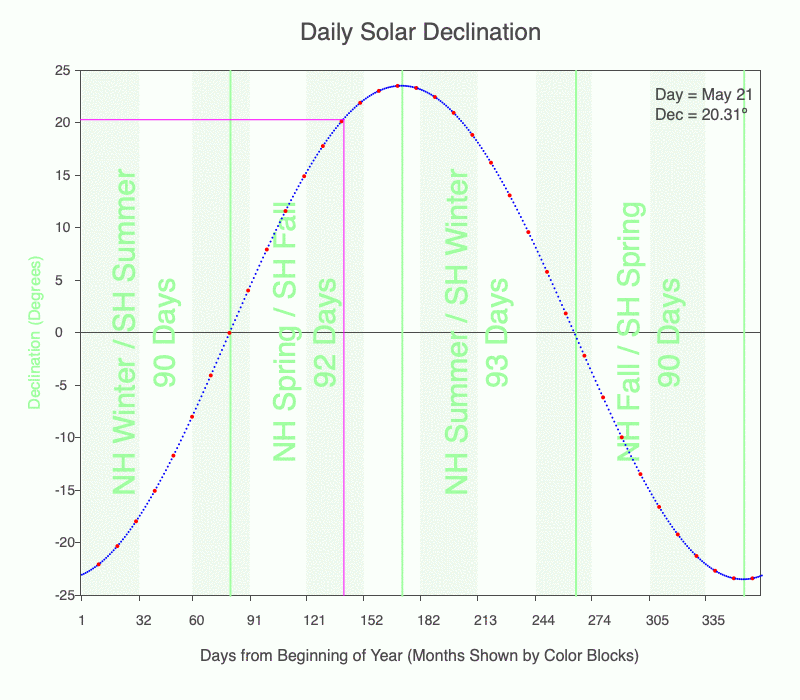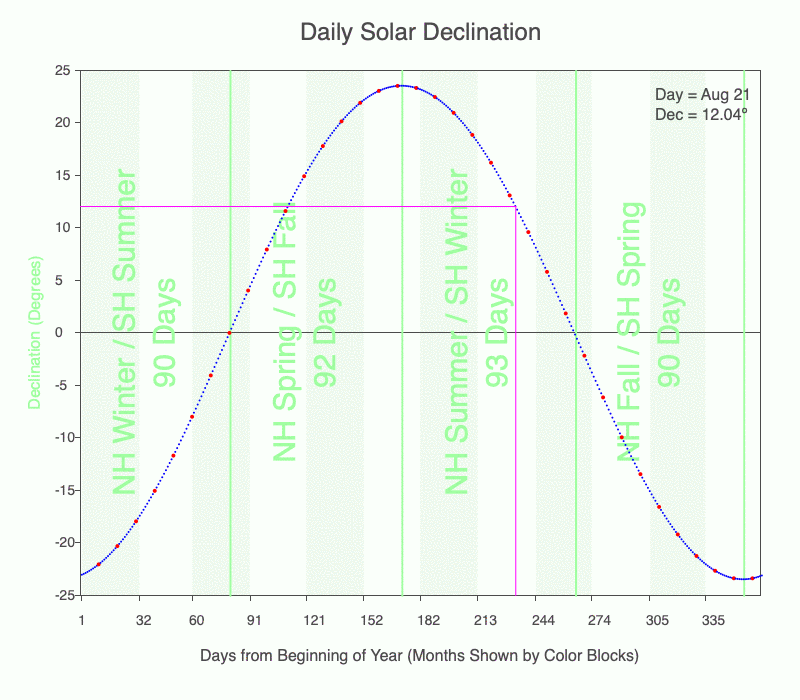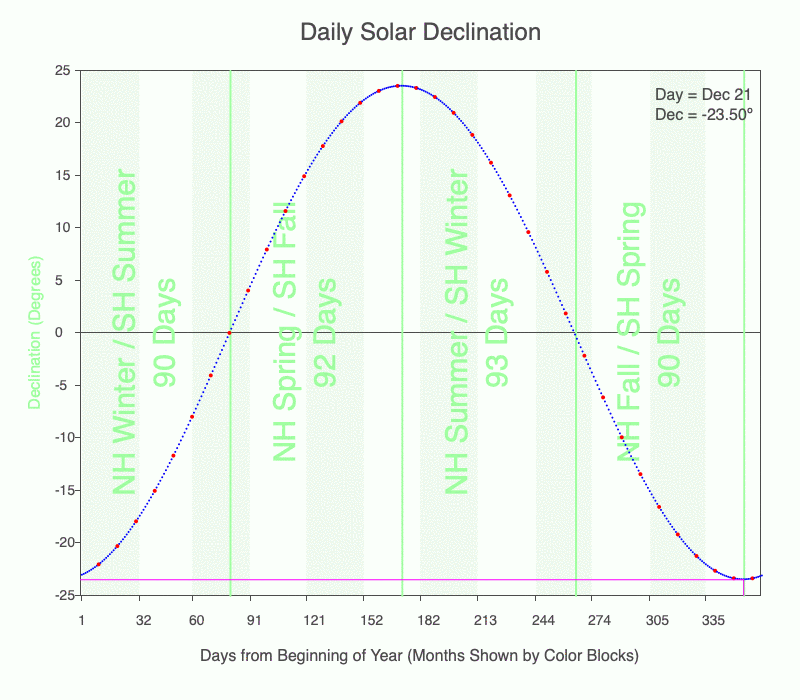
Use the graph of daily solar declination to calculate the direction of the local noon shadow. Every tenth day is marked with a red dot. Months are shown with alternating light green and white stripes. Darker green vertical lines mark the seasons. Download a pdf of the graph to print if you like.
Using the Sun and Shadows as a Clock
Although a shadow trace shows how the shadows move throughout the day, we often don’t have this available at a snapshot in time. The more familiar you are with how shadow traces change at a given latitude at different times of the year, the easier it is to envision the complete shadow trace from one shadow at a particular time of the year. Below are the hourly shadow positions for 45ºN at three times of the year: December 21, March 22, and June 21. Compare these animations to the shadow traces for 45ºN every 30 days throughout the year.
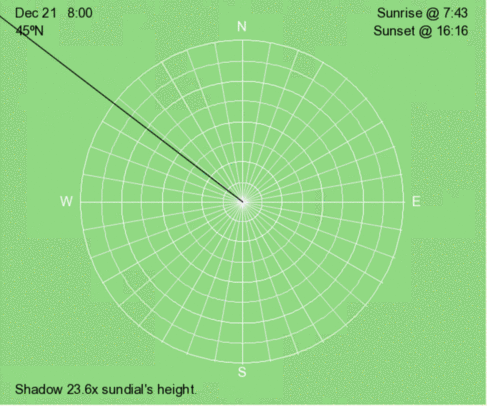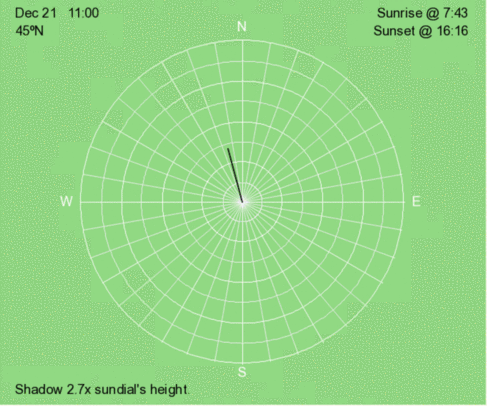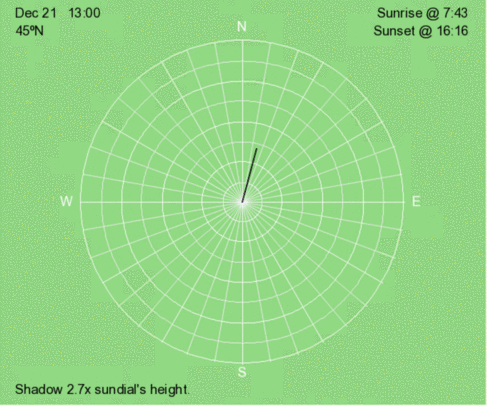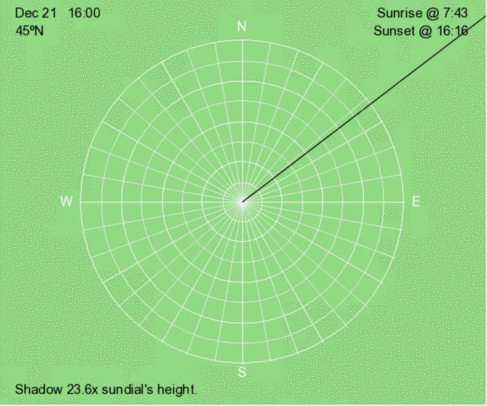
Hourly shadow motion during December 21 at 45ºN.
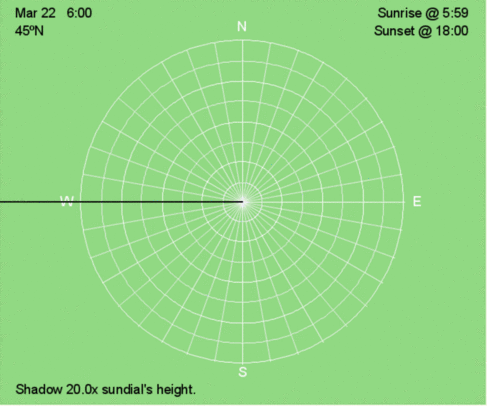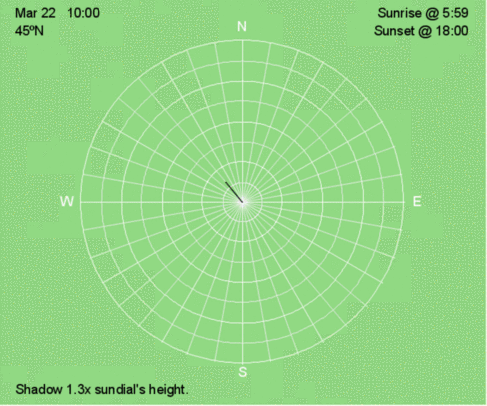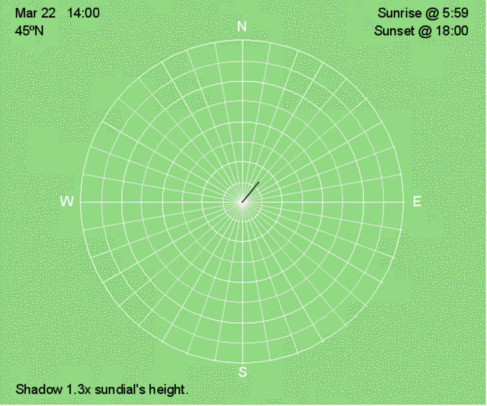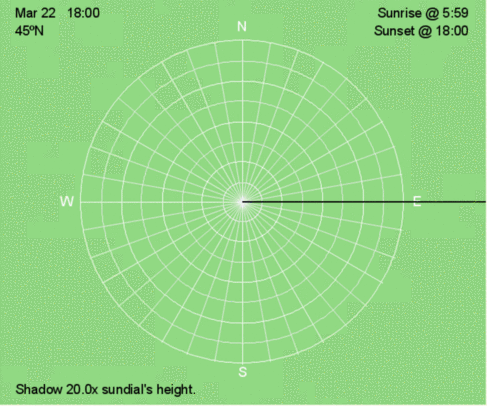
Hourly shadow motion during March 22 at 45ºN.
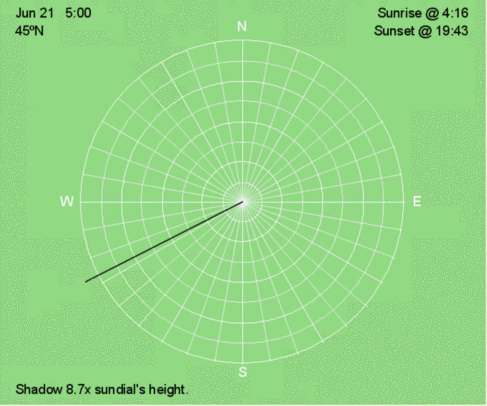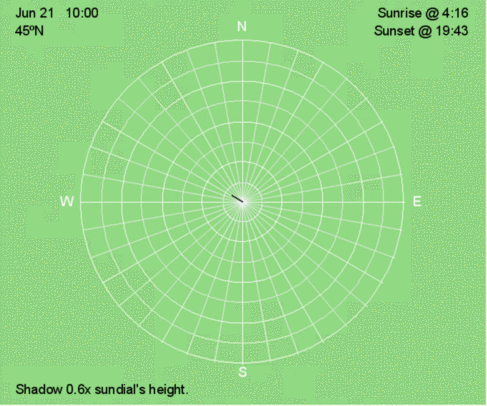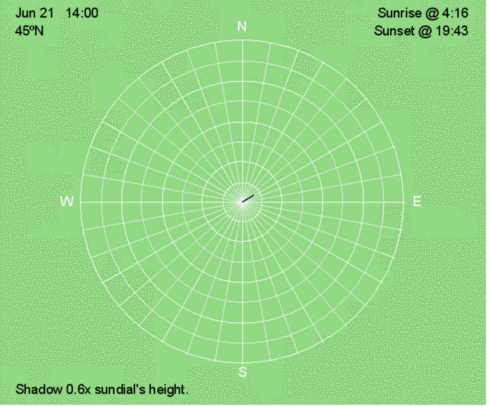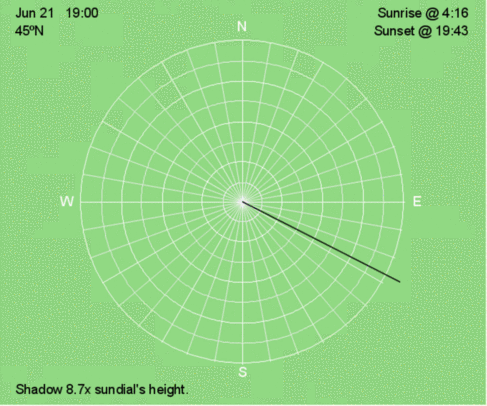
Hourly shadow motion during June 21 at 45ºN.
Key Patterns of Shadows as a Clock
- Since the Earth rotates from west to east, the Sun appears to move with a westward component throughout the day. This means that shadows appear to move with an eastward component. Before local noon, shadows are west of north/south, and after local noon, shadows are east of north/south.
- Near local noon, shadows have the most consistent eastward movement.
- Shadows decrease in length from sunrise to local noon and increase from local noon to sunset.
Above are shadow traces for 45ºN every 30 days throughout the year.
Using the Sun and Shadows as a Calendar
In the Northern Hemisphere, shadows before and after local noon are longer than the previous day’s between the June 21 solstice and the December 21 solstice. On the other days, shadows are shorter than the previous day’s.
In the Southern Hemisphere, the opposite trend occurs for morning and afternoon shadows. Shadows are shorter the previous day’s between June 21 and December 21.
The above trends hold for local noon shadows when poleward of the Tropic Circles (23.5ºN and 23.5ºS). Since the Sun will be directly overhead at local noon twice a year, and there won’t be a shadow at these times. These occur when:
latitude + declination = 0º.
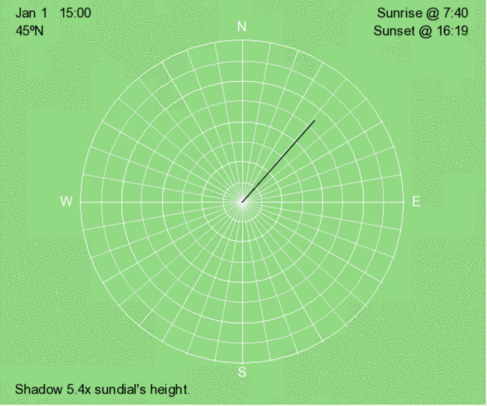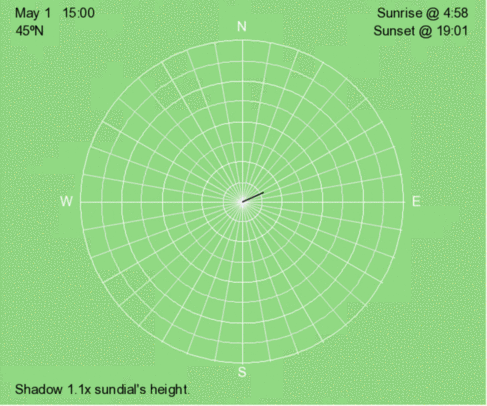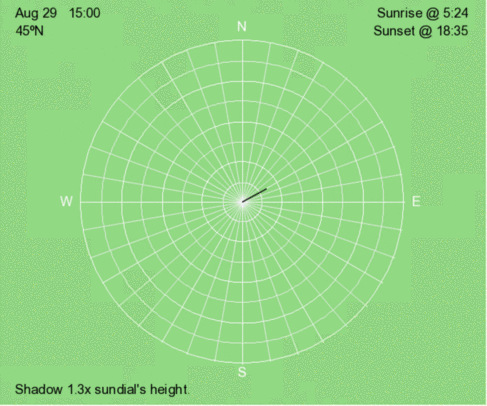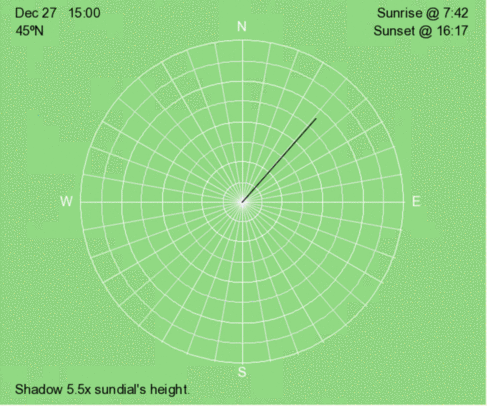
Above is an animation of the shadow that occurs at 3 PM (solar time) at 45ºN every 30 days throughout the year.
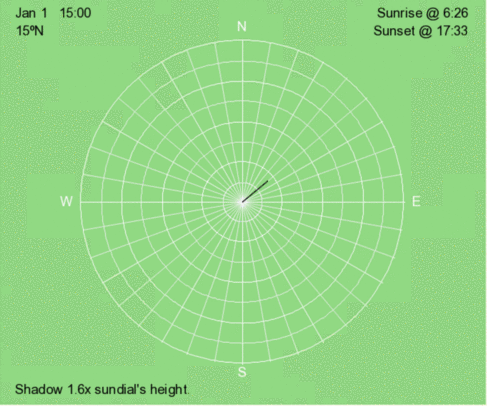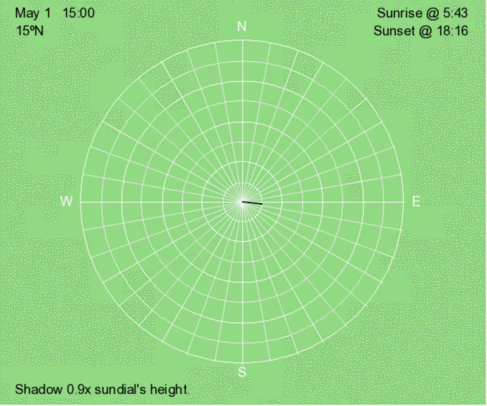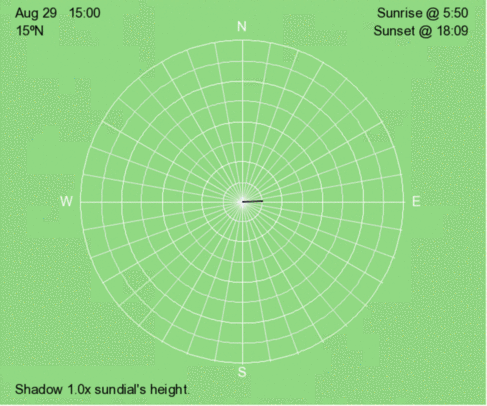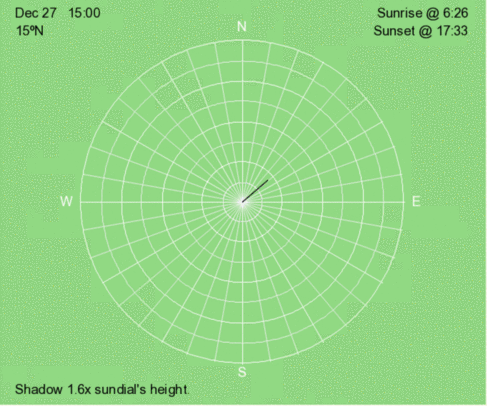
Above is an animation of the shadow that occurs at 3 PM (solar time) at 15ºN every 30 days throughout the year.
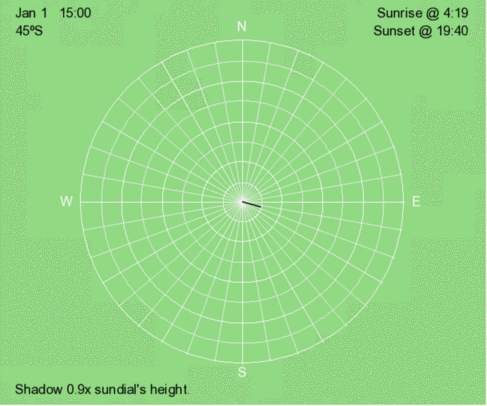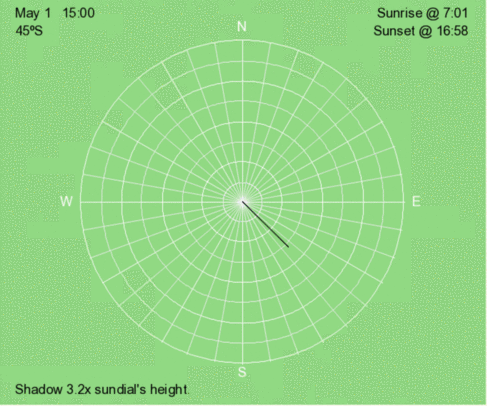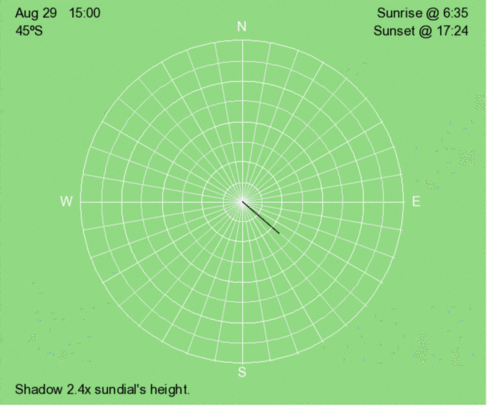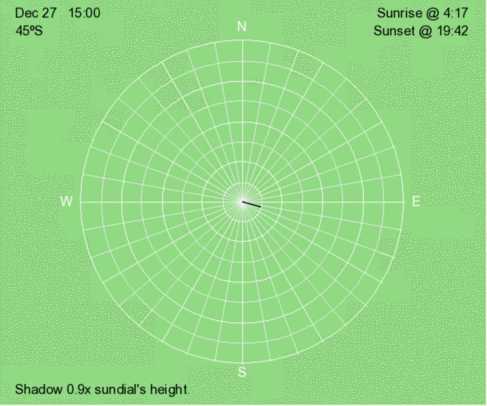
Above is an animation of the shadow that occurs at 3 PM (solar time) at 45ºS every 30 days throughout the year.
Big Ideas
- Sundials create shadows that make it easier to use the Sun’s position to navigate and tell the time, day, and season.
- Clock time that humans use does not equal solar time measured by sundials.
- Since the Earth rotates from west to east, the Sun appears to move with a westward component throughout the day. This means that shadows appear to move with an eastward component.
- Shadow length and direction depend on the latitude, day, and time.
- When the Sun is highest in the sky, it crosses the local longitude, oriented north/south. At local noon, the shadow is either pointing north or south, unless the Sun is directly overhead and there won’t be a shadow.
Click on the following toggles to view descriptions and links of the web pages on each topic of the Sun-Earth Connection.
Sun-Earth Connection overview
An overview of how the Sun’s energy is generated and how its thermal radiation illuminates and heats Earth.
Earth Illumination Patterns
- Overview: The Sun illuminates the spherical, rotating planets orbiting it.
- Obliquity and Earth’s Illumination: Obliquity is the angle between the planes of the Earth’s equator and its orbit around the Sun.
- Declination, Latitude, & Earth Illumination: Solar declination is the angle between the Sun’s rays and the plane of the Earth’s Equator. Its value depends on where Earth is in its orbit around the Sun.
- Astronomical Seasons & Illumination: Astronomical seasons are based on the orientation of Earth’s axis of rotation to the Sun, which determines the amount of illumination between the Northern and Southern Hemispheres.
Distribution of the Sun's Energy on Earth
- Overview: Even though an area is illuminated by sunlight, there can be quite a range of energy interacting with the surface.
- Sun Angle and Beam Concentration: If every beam of sunlight reaching Earth has the same amount of energy, why do some areas warm up more than others?
- Diurnal Heating: Diurnal heating is the temperature change over 24 hours. When sunlight shines on the ground, it warms. Two critical factors that determine the amount of heating deal with the Sun’s illumination.
- Seasons: Earth experiences astronomical seasons due to its obliquity.
- Climate Regimes: Climate regimes are an extension of diurnal heating and seasons, but the time frame is now years.
Declination Circles: A tool to analyze the Sun's position in the sky.
- Overview: Drawings of declination circles contain the visual and numerical information to understand and predict the Sun’s motion across the sky.
- Declination Circles 101: Draw a declination circle with just a ruler and protractor/compass to quickly and accurately know the Sun’s position in the sky at any day and time of the year for any location on Earth.
- Drawing Declination Circles: Declination circles are quite easy to draw by hand.
- Interpreting Time on Declination Circles: Accurately estimate the time of day using the Sun’s location in the sky.
- Sunrise, Sunset, & Twilight: Calculate the timing and duration when the Sun is at or near the horizon.
- Solar Time, Angle, & Position: The sun’s angle and direction to the local horizon define the Sun’s position in the local sky. Explore how to use declination circles to calculate the Sun’s position at any solar time anywhere in the world on any day of the year.
- Changing Views of Declination Circles: Use the web app View Declination Circles to explore three common views of declination circles to identify their strengths, limitations, and applications. Then learn how to go from one view to another.
- Using Declination Circles: Humans have been using the apparent motion of the Sun as a compass, clock, and calendar for millennia.
- Using Sundials: Humans have been using the Sun’s position to navigate and tell the time, day, and season for millennia. Sundials create shadows that make it easier to do these tasks.

0 Comments