Air Parcels and the Ideal Gas Law
Air Parcels
The soda-bottle cloud experiments on the previous page provided a visualization of how meteorologists work with air changing position on Earth: air parcels. This model assumes individual volumes of air are separated from each other by thin, expandable barriers so that the parcel retains its shape but may change size as it changes temperature and altitude. These barriers block the mixing of energy and molecules between parcels. A process that does not exchange energy or mass with the surrounding environment is adiabatic. This model doesn’t apply to all processes in the atmosphere, but it does work well for most. Air parcels help meteorologists model the changes to the gas inside the parcel as it moves rather than analyze the many bundles of air moving past a fixed point on Earth.
An air parcel has flexible barriers that block the mixing of energy and molecules between other air parcels.
Air Pressure
Air pressure is proportional to the weight of the column of air above that location and elevation. We often forget we are at the bottom of our atmosphere, a gaseous envelope around our planet.
The weight of the air above compresses the air below, so the density of air increases going toward the surface and air pressure decreases exponentially with altitude.
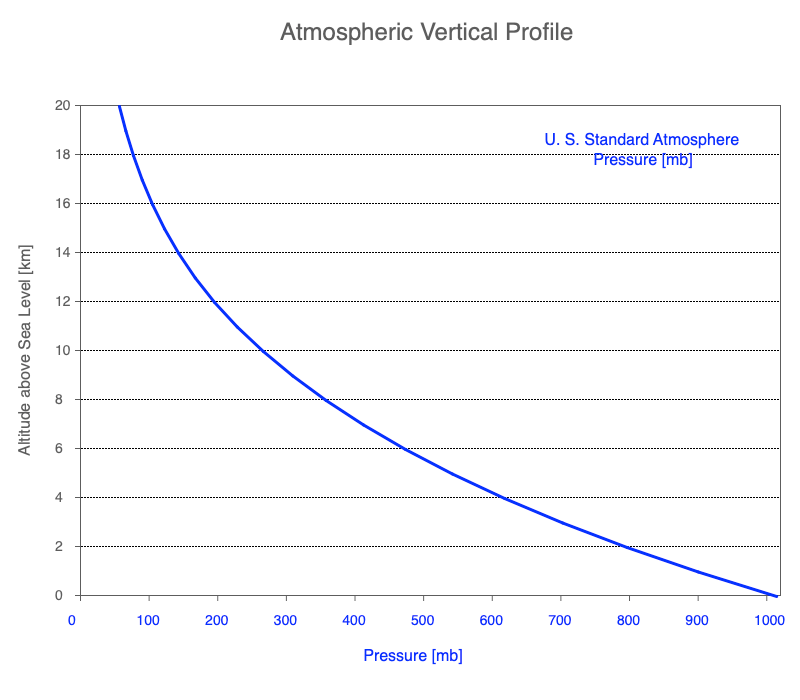
Air pressure decreases exponentially with altitude.
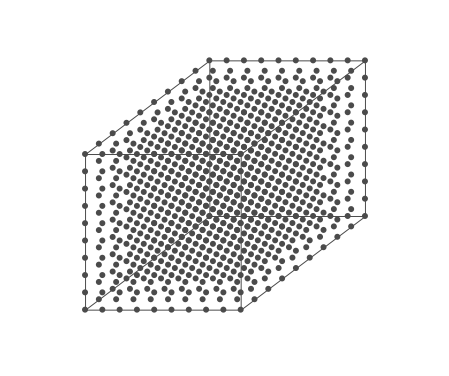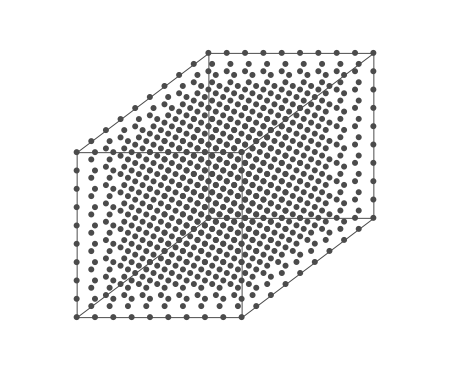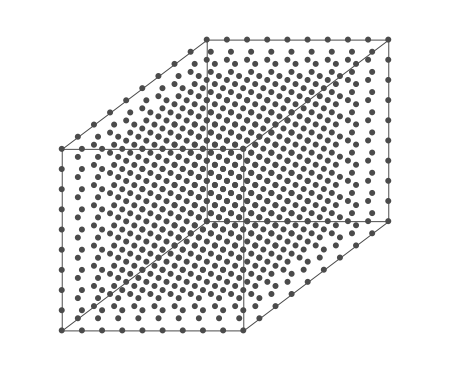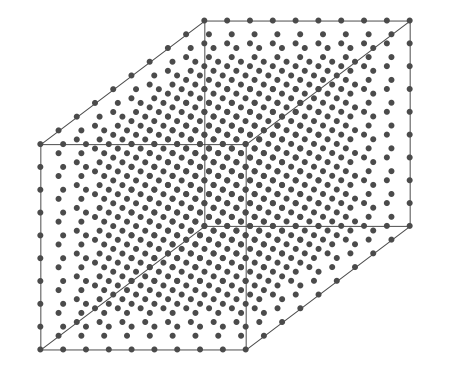
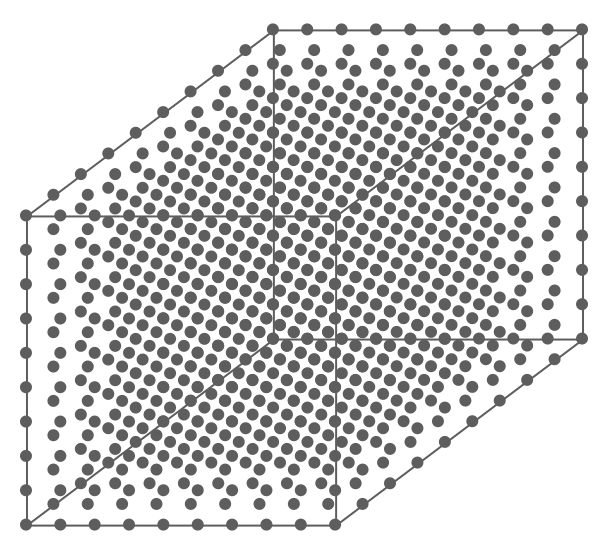
Above is an air parcel that is expanding as it rises from the ground to the top of the troposphere. Since the spacing between the molecules increases as the volume expands, the air parcel density decreases as the parcel rises in the atmosphere.
Ideal Gas Law
Gases rise and sink in our atmosphere, so they move from high to low air pressure. The effects of changing altitude are calculated using the Ideal Gas Law:
PV = nRT
Where
- P is the air pressure acting on the walls of the parcel from both the outside and inside. As the parcel changes altitude, the pressure acting on the parcel changes – and conditions within the parcel must change, so the pressure exerted from the inside of the parcel equals the pressure on the outside. Air pressure on the outside of the parcel is the weight of the column of air extending above the parcel.
- V is the volume of the air parcel, and given that we are using a cube, it is straightforward to visualize.
- n is the number of air molecules inside the parcel (actually, it is the number of moles if doing calculations with the equation).
- R is the ideal gas constant, and since it doesn’t change, we will not discuss it any further.
- T is the temperature of the air molecules, which is proportional to the average kinetic energy of the molecules (0.5 * mass of molecule * speed of molecule²).
- Note that RT represents the average kinetic energy of the molecules.
Ideal versus Non-Ideal Gases
Ideal gases involve molecules that have no attraction between each other, and they don’t have a volume, both of which don’t occur in nature. However, the Ideal Gas Law works well for gases at Earth’s atmosphere’s temperatures and pressures, at least those within 25 km of the Earth’s surface. So for our needs, this equation is handy. To explore when gases act as non-ideal, see this site.

Squeeze a 2-liter soda bottle of air with an LCD thermometer inside to see the temperature change.
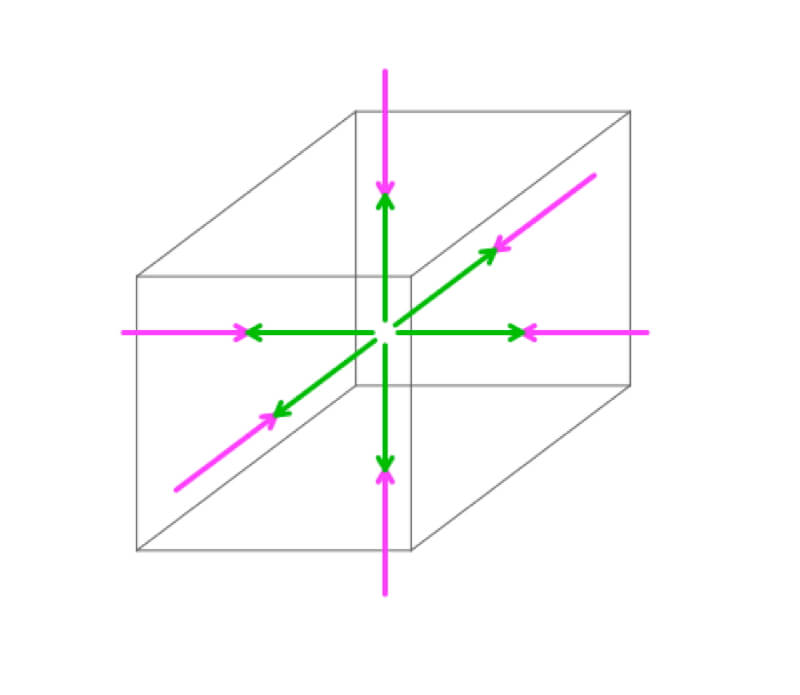
An air parcel changes volume so the air pressure within the parcel (green) is equal and opposite the air pressure acting on the outside (magenta). See the activities on balanced forces to explore these concepts further.
The Ideal Gas Law and Air Density
Mathematically manipulating the Ideal Gas Law lets us calculate the density of a given amount of air, which determines whether air rises and sinks in the atmosphere. To explore the math, see Chapter 1 of Roland Stull’s free on-line book, Practical Meteorology: An Algebra-based Survey of Atmospheric Science.
Since density is mass/volume, there are two ways to change the density of the gas: add mass or alter the volume. The Ideal Gas Law shows that increasing air temperature increases the volume of the air parcel (see the animation), so the air density decreases at temperature increases.
Water vapor (H2O) is the most variable molecule entering and exiting the atmosphere. It is one of the lightest molecules in the air, especially compared to the dominant gases, diatomic nitrogen (N2) and oxygen (O2). When water vapor increases, the amount of oxygen and nitrogen decrease per unit volume (the term n in the Ideal Gas Law remains constant), which lowers the mass and decreases the air’s density.
Two components determine air density: temperature and chemical composition, but the temperature has a dominant effect compared to the amount of water vapor (see the graph that follows). In the Ideal Gas Law and Clouds, we will explore the role of water vapor in much more detail. For this page, we will focus solely on the effects of temperature on an air parcel’s density.

In this animation of 1000 evenly spaced molecules in a cubic volume, the temperature increases from 0 to 30°C, which causes the parcel to expand.
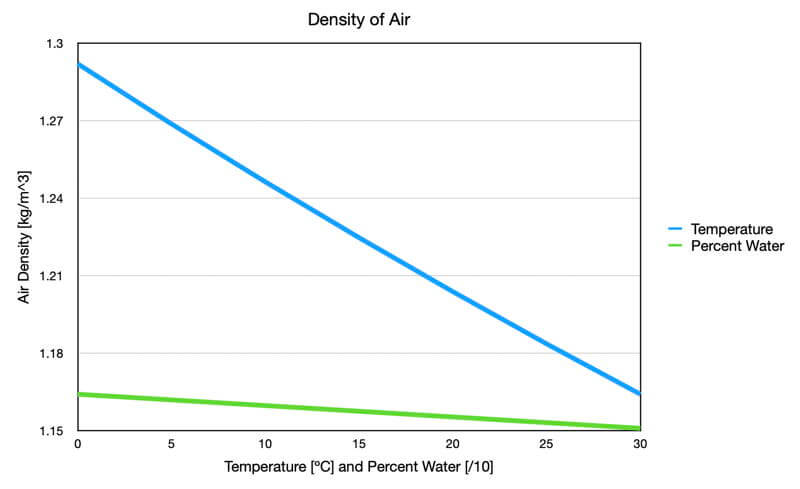
Graph showing the effect of temperature (blue) and percent water vapor (green) on air density. The temperature data used dry air, and the water vapor data used an air temperature of 30C. Both were at standard surface air pressure. Notice that the temperature has a dominant impact on air density.
Rising Air and the Ideal Gas Law
An air parcel’s walls act as a barrier for mixing, so we will assume that the number of molecules inside the parcel (referred to as ‘n’) stays constant throughout the air’s movement. When air changes altitude, it experiences a change in pressure and expands or compresses accordingly. If the parcel rises, its volume increases, but at a rate that depends on the length of the parcel’s side cubed. The volume increases at a slower rate than the decrease in pressure, so the term PV decreases. Since n and R are not changing, that means the temperature, T, must drop. Conversely, if the parcel sinks toward the Earth’s surface, pressure increases, volume decreases but at a slower rate than pressure, and PV increases. Sinking air warms.
Working through the math, we find that a rising parcel of air without condensation occurring cools at 9.8ºC/km, and sinking air heats up at the same rate. This temperature change with height is the dry adiabatic lapse rate. If an air parcel’s rise and fall are adiabatic (no exchange of heat and mass with the surrounding air), the parcel’s temperature will be the same when it returns to the ground.
The heating of the air parcel changes dramatically when water vapor condenses and evaporates within it. These effects will be explored in the Ideal Gas Law and Clouds.

Use the Ideal Gas Law to calculate the temperature within a rising or sinking parcel of air. In this example, energy and mass within the parcel are not exchanged with the surroundings.
Expanding + Cooling = Decrease in Density?
Analyzed separately, an expanding volume would create a decrease in density, but cooling an object (other than water between 0 and 4°C), increases its density. The key to understanding the dominant effect on an air parcel’s density as it rises or sinks is to examine the percent change of pressure and temperature in the Ideal Gas Law.
The animation above is misleading since the units are not the ones used in the Ideal Gas Law. Pressure should be converted to Pascals, where 1 Pa = 0.01 mb. In the animation, pressure decreases 50 mb each frame, or 5000 Pa, so there is a minimum percent change of 5% (= 5,000/100,000). The temperature needs to be converted to Kelvin, where K = °C + 273.15. As the parcel ascends from 1000 to 950 mb, the temperature decreases 5.1K/(9.0ºC+273.15) = 1.8%. This means that decreasing pressure has a greater effect on the air parcel’s volume, and hence, its density, than decreasing temperature as air rises or sinks in the atmosphere.

0 Comments