Coriolis and Centrifugal Forces
Earth is a rotating sphere which creates uneven heating patterns across its surface (see the Sun-Earth Connection) but also affects every moving liquid and gas on Earth. To be accurate, the fluids should flow roughly a mile without interacting with a solid, so our bathtubs, sinks, and toilets are off-limits.
Coriolis Force
Earth’s Rotation
Earth is a rotating sphere, and how fast an object moves depends on its distance from the axis of rotation. Since the axis of rotation intersects the Earth’s surface at the poles, when standing on the North Pole, you aren’t moving due to Earth’s rotation. The fastest one can move on Earth is at the Equator, the furthest from the axis of rotation. If you have played on a merry-go-round, it was quite easy to be in the center, but quite a challenge to hold on at the edge!
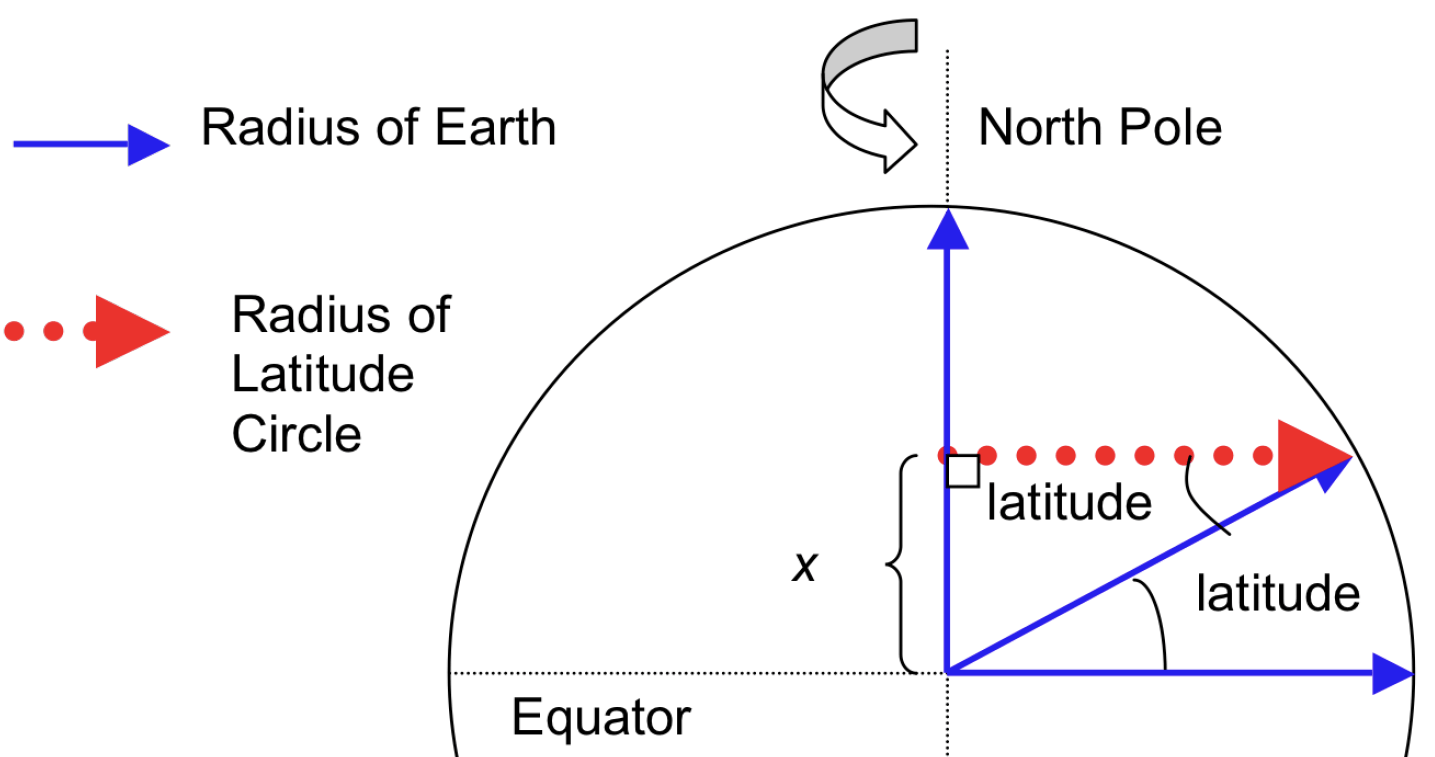
Illustration showing the radius of a latitude circle is the perpendicular distance from the Earth’s axis of rotation to the latitude on the surface of the Earth. Going toward a pole, we get closer to the axis of rotation, and when we move toward the Equator, we get further away.
Speed is the distance traveled divided by the time of travel. The circumference of a circle is 2 * π * radius. The Earth’s radius is 6371 km, which means someone standing on the equator is moving at 40,0030 km / 24 hours = 1668 km/hr = 1036 mph. And we don’t even notice! Yet someone standing on the South Pole would not be moving.
Notice in the graph of the speed from Earth’s rotation that the change in how fast we are moving is not linear. Speed of rotation changes most quickly at the poles and very little at the Equator. Since the speed of rotation is 2 * π * 6371 km * cos(latitude) / 24 hours, this graph is a version of the cosine function.
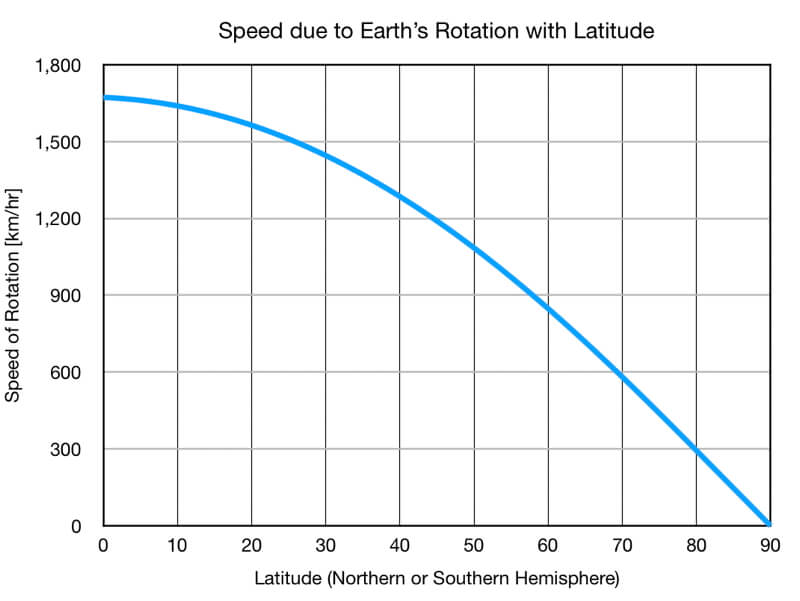
Graph of how fast we are moving on our rotating Earth based on our latitude. Standing at the North or South Pole would be a very slow pirouette that takes a day to complete – and we aren’t actually moving in space. Yet at the Equator, we are moving at a brisk 1667 km/hr (over 1000 miles per hour)!
Angular Momentum
When an object changes latitude, it changes the distance to the axis of rotation, and this is where we need to explore angular momentum. Momentum, equal to an object’s mass times velocity, is a quantity that measures how difficult it will be to stop a moving object. Imagine trying to stop a shopping cart pushed at you from across an aisle, and that of a two-ton truck moving at the same speed. It is much easier to stop the cart compared to the truck. But if the cart were moving at highway speeds, this would be much harder to stop than at lower speeds.
Rotating objects also have a version of momentum, but it is called angular momentum, and it indicates how difficult it will be to stop the object from rotating. Angular momentum is calculated by multiplying the momentum by the radius of rotation, so mass x velocity x radius. In this case, the velocity is the tangential velocity or the speed at any point during the rotation.
Momentum and angular momentum have an important property: they remain constant unless acted upon by an unbalanced force. For rotating objects, this is the conservation of angular momentum. When an ice skater goes into a spin and they pull in their arms and legs inward, they spin faster. They slow down when they move their limbs away from the axis of rotation. In all cases, the skater’s angular momentum is constant. As the radius of the skater decreases, they spin faster, and as their radius increases, they rotate slower.
See additional information on angular momentum.
The End Result: Coriolis Force
Since Earth is rotating, water and gas on or above its surface have angular momentum. When a fluid moves from one latitude, it changes the distance from the axis of rotation, so the rate of rotation changes to maintain constant angular momentum. We’ll focus on air, but the following applies to any fluid moving along the Earth’s surface or objects traveling through the atmosphere. Explore movies of water in a rotating water tank to explore how fluids move on any planet.
As pressure gradient force (PGF) pushes air toward the poles, it gets closer to the axis of rotation, and as with the skater, the air moves faster in its west-to-east motion, moving to the east of the air it is moving into. And when air moves toward the equator, it slows its west-to-east motion and moves to the west of the air it is moving into. When looking along the initial path of the northward or southward push, in the Northern Hemisphere, the air moves to the right. In the Southern Hemisphere, the air moves to the left of the initial push.
But what about the air that moves initially to the west or east? It is staying at the same latitude, so it isn’t changing its distance to the axis of rotation. In the case of moving eastward, the air will be moving faster than it needs to stay at the Earth’s surface, it moves perpendicularly away from the axis of rotation (see spinning marshmallow activity). Gravity pulls the air back to the ground, but this is toward the center of the Earth, so the air moves toward the equator. The air moves to the right of the eastward push in the northern hemisphere and to the left of the push in the southern hemisphere.
When air moves westward, it is moving slower than air that would stay at the same distance from the axis of rotation, so it would move perpendicularly toward the axis. But the ground gets in the way, and the slope of the surface would push it toward the poles (remember the air is not sinking toward the Earth’s center but perpendicular to the axis of rotation). And, as with the other cases, the air is moved to the right of the westward push in the northern hemisphere and to the left in the southern.

A movie of a simple experiment in the conservation of angular momentum. Tie a weight on a string, thread the line through a straw. Start spinning the mass around the straw. Pull the string through the straw while keeping the straw still. The spinning weight speeds up as the distance to the axis of rotation decreases!
For safety, rather than using a metal nut, tie a marshmallow or a felt ball to the string.
Notice that the only time the eastward or westward pushed air won’t bend is at the equator since the gravitational pull toward the center of the Earth and the perpendicular direction to the axis of rotation are parallel. This gives an indication that there isn’t a Coriolis force acting on air moving along the equator, so there must be a relationship between latitude and the magnitude of Coriolis force. Coriolis force is proportional to sin(latitude), so it is at a maximum at the poles (sin 90º = 1) and zero at the equator (sin 0º = 0). In calculations, meteorologists use the Coriolis coefficient which is 2 x Earth’s rate of rotation * sin(latitude).
Coriolis force is always perpendicular to the wind and is proportional to the wind’s speed (there isn’t any Coriolis force acting on air that isn’t moving).
For more detail, see this supporting article on Coriolis force.
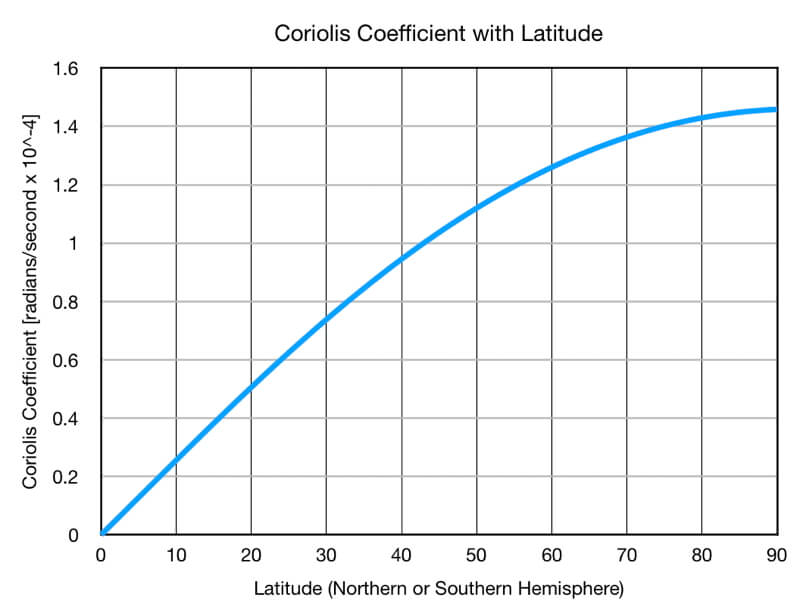
Coriolis coefficient with latitude. Essentially this is a constant times the sine of the latitude.
Centrifugal Force: When the Wind Changes Direction
Centrifugal force is an apparent force that results from an object to resist a change in direction. If we swing a marshmallow tied to a string, we feel a “force” pulling the marshmallow outward. It isn’t an actual force, rather, you feel the effect of creating the inward-pointing centripetal force.
Since air isn’t tied to a string, centrifugal force acts on the air in the direction outward from the radius of curvature.
The magnitude of the centrifugal force is proportional to the wind speed (increases as wind speed increases) and inversely proportional to the radius of curvature (increases as the radius of curvature decreases).
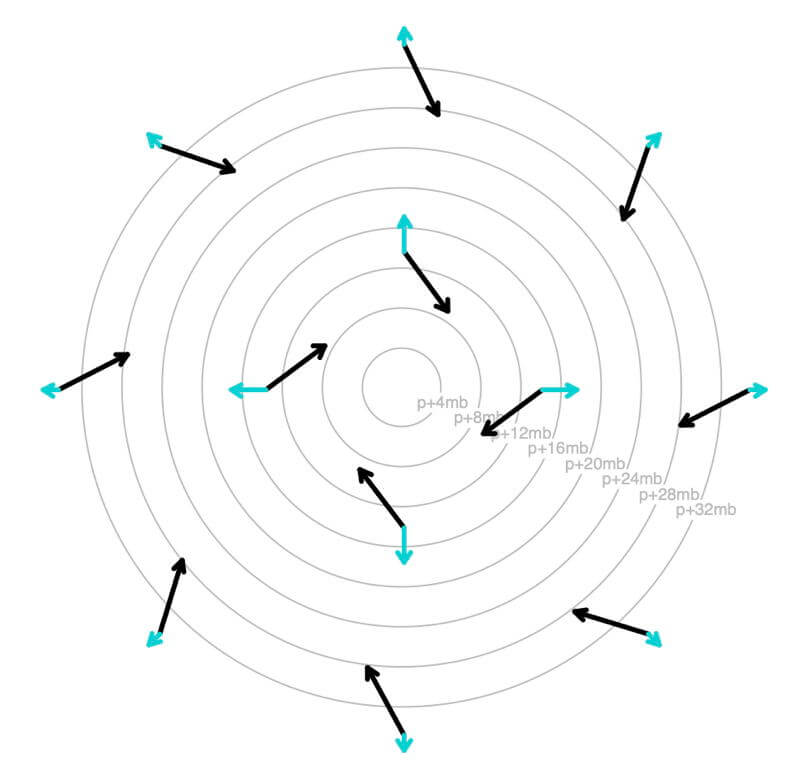
An illustration of wind (black arrows) as it moves around a circular low-pressure center. The centrifugal force acting on the moving air is in cyan (blue-green).
As air is pushed toward the center of a low-pressure center, is curves, creating an outward-directed centrifugal force.
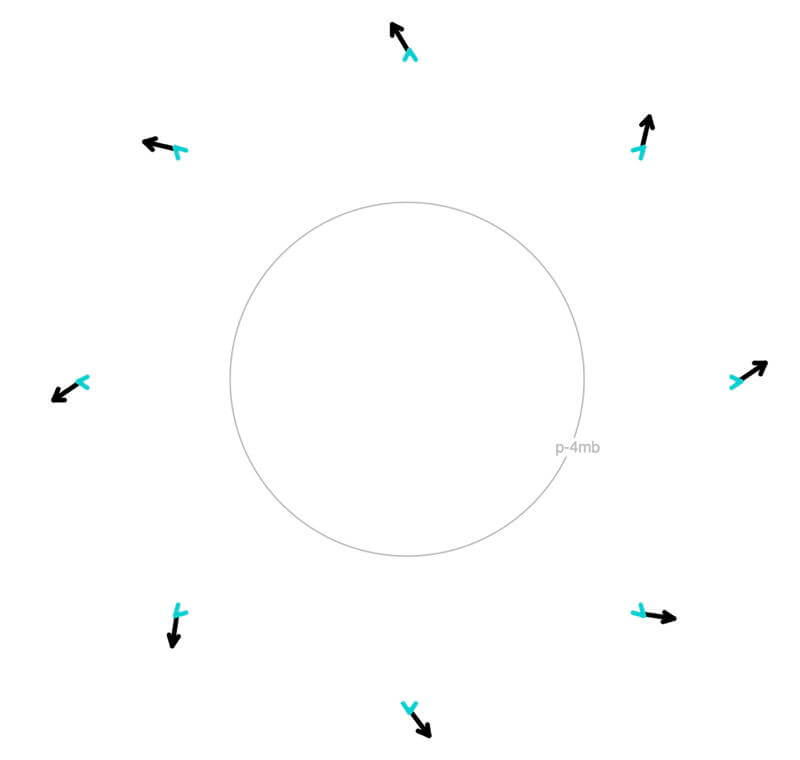
As air is pushed away from the center of a high-pressure center, it curves (see black wind vectors), creating an outward-directed centrifugal force (cyan).
Centrifugal force is always acting away from the wind’s center of curvature.

0 Comments